
Question and Answers Forum
AlgebraQuestion and Answers: Page 230




Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234
|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 230 |
| b, x, y, c are consecutive terms of a G.P. ∴ x = br, y = br^2 , c = br^3 A.M. between b and c is a ∴ ((b+c)/2) = a ⇒ 2a = b+c 2abc = (b+c)bc = b^2 c + bc^2 = b^2 (br^3 ) + b(br^3 )^2 = b^3 r^3 + b^3 r^6 = (br)^3 + (br^2 )^3 = x^3 + y^3 ∴ x^3 + y^3 = 2abc ← |
| What condition should be satisfied by the vectors a and b for the following relations to hold true :(a)∣a+b∣=∣a−b∣ ;(b)∣ a+b∣>∣ a−b∣;(c)∣a+ b∣< ∣a−b∣ |
| (26) OA^(→) = a^→ = (((4.8)),((3.6)) ) , OB^(→) = b^→ = ((( 8)),((15)) ) a^→ . b^→ = (4.8)(8) + (3.6)(15) = 92.4^(→ ) a = (√(4.8^2 +3.6^2 )) = (√(23.04+12.96)) = (√(36)) = 6 b = (√(8^2 +15^2 )) = (√(64+225)) = (√(289)) = 17 a.b = 6 . 17 = 102 cos AOB = ((a^→ .b^→ )/(a.b)) = ((92.4)/(102)) = 0.9059 = cos 25.06° ∴ ∠AOB = 25.06° |
| (23) Let a^→ = ((( 7)),((24)) ) and b^→ = ((( 3)),((−4)) ) a^→ .b^→ = (7)(3) + (24)(−4) = 21−96 = −75 a = (√(7^2 +24^2 )) = (√(49+576)) = (√(625)) = 25 b = (√(3^2 +(−4)^2 )) = (√(9+16)) = (√(25)) = 5 a.b = 25 . 5 = 125 Let θ be the angle between a^→ and b^→ . cosθ = ((a^→ .b^→ )/(a.b)) = ((−75)/(125)) = −0.6 = cos126.87° ∴ θ = 126.87° |

|

|
| If x = (√(42−(√(42−(√(42−...)))))) y = (√(x+(√(x+(√(x+...)))))) z=(√(y.(√(y.(√(y.(√(y...)))))))) . Find x+y+z . |
| solve in N: b^3 (2b^2 +2b+1)=18360 |
| Given A=n^2 −2n+2 , B=n^2 +2n+2 n ∈ N^∗ −{1}. Show that ∀ divisor of A which divise n can also divise 2. Show that all common divisor of A and B can divise 4n. |
| factorise x^4 +4 |
| find all numbers >1 from N which their cube are <18360 |
| show that if n is odd , n(n^2 +3) is even. |
| Find the area of a rhombus with side 8 cm |
| ..calculus.. x,y,z ∈R^+ and x^2 +y^2 +z^2 =1 find min_(x,y,z∈R^(+ ) ) ((((yz)/x)+((xz)/y)+((xy)/z)) )=? m.n.1970.. |

|
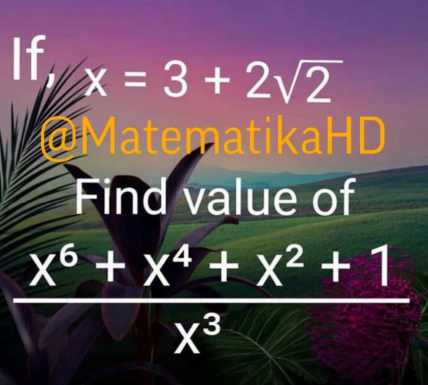
|
| If f(x) is a polynomial function satisfying the relation f(x)+f((1/x))=f(x)f((1/x)) for all 0≠x∈R and if f(2)=9, then f(6) is (A) 216 (B) 217 (C) 126 (D) 127 |
| The number of surjections of {1,2,3,4} onto {x,y} is (A) 16 (B) 8 (C) 14 (D) 6 |
| Let f : [1,∞)→[2,∞) be the function defined by f(x)=x+(1/x) If g : [2,∞)→[1,∞), is a function such that (g○f)(x)=x for all x≥1. Show that g(t)=((t+(√(t^2 −4)))/2) |
| 1)((√3)−1)((√3)+1)=(√3)×(√3)−(√3)−1 =3−(√3)−1 =2−(√3) 2)(2x+(√3))(2x−(√3))=(2x)^2 −2x(√3)+2x(√3)−3 =4x^2 −3 |

|
| Log (cosβ) = p ⇒ cos β = 10^p ∴ secβ = (1/(cosβ)) = (1/(10^p )) = 10^(−p) ∴ Log (secβ) = Log 10^(−p) = −p Log 10 = −p |
| x^2 +y_ ^2 =a^2 (√(2 )) x^2 +y^2 =a^2 what is intersection Angle=? |

|
| Let P(x) be a polynomial function of degree n such that P(k)=(k/(k+1)) for k=0,1,2,...,n. Then P(n+1) is equal to (A) −1 if n is even (B) 1 if n is odd (C) (n/(n+2)) if n is even (D) (n/(n+2)) if n is odd Which among the four proposals is/are correct ? |
| Let f : R→R be a function satisfying the following : (a) f(−x)=−f(x) (b) f(x+1)=f(x)+1 (c) f((1/x))=((f(x))/x^2 ) for all x≠0 Show that (i)f(x)=x for all x,y∈R (ii) f(x+y)=f(x)+f(y) for all x,y∈R (iii) f(xy)=f(x)f(y) for all x,y∈R (iv) f((x/y))=((f(x))/(f(y))) for all x,y∈R with y≠0 |
Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 |