
Question and Answers Forum
AlgebraQuestion and Answers: Page 323





Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327
|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 323 |
| x^x =2 find the value of x. |
| ((√(2)^(√2) )) |

|
| let A = (((1 −1 0)),((−1 1 1)) ) (0 0 3 ) calculate A^n . |
| let A = (((0 1 1)),((1 0 1)) ) (1 1 0 ) 1) calculate p_c (A) the caracteristic polunom of A 2) calculate A^n with n integr natural 3) calcypulate e^(tA) t∈ R |
| let A = (((1 −2)),((1 4)) ) calculate A^n 2) find e^A , e^(−A) 3) find e^(iA) , e^(−iA) and e^(iA) +e^(−iA) . |
| E id k vectorial space and f∈L(E) 1)prove that if f is nilpotent with indice p≥1 ,I −f is bijective and (I−f)^(−1) =Σ_(i=0) ^(p−1) f^i 2)let E=R_n [x] and f∈L(E) / f(p) =p−p^′ prove that f is inversible and find f^(−1) . |
| if 3x^2 +2αxy+2y^2 +2ax−4y+1 can be resolved into two linear factors, prove that ′α′ is a root of the equation x^2 +4ax+2a^2 +6=0 |
| if α , β are the roots of the quadratic equation ax^2 +bx+c =0 then find the quadratic equation whose roots are α^(2 ) , β^2 |
| let f(x) = e^(−x^2 ) 1) prove that f^((n)) (x)=p_n (x)e^(−x^2 ) with p_n is a polynom 2) find a relation of recurrence between the p_n 3) calculate p_1 ,p_2 ,p_3 ,p_4 |
| p is a polynome having nroots simples x_i (1≤x_i ≤n ) with x_i ^2 ≠1 calculste Σ_(k=1) ^n (1/(1−x_k )) . |
| let p(x)=x^3 −2x^2 −1 and α is root of p(x) prove that α∉ Q . |
| p is apolynom with n roots differents let Q = p^2 +p^′ let α the number of roots of Q prove that n−1≤α≤n+1 . |
| 1)decompose inside C[x] p(x)=x^(2n) −2(cosα)x^n +1 2) decopose p(x)inside R[x] |
| prove that 2^(n+1) divide [(1+(√3))^(2n+1) ] [x] mean integr part of x |

|
| find the sum of 4 digit even numbers formed from the digit 1, 2, 3, 4 |
| lim_(x→∞) (x^x^x^(.....) ) |

|

|
| if y=tan^(−1) x show that (1+x^2 )y_(n+2) +2(n+1)xy_(n+1) +n(n+1)y_n =0 |
| x^3 +y^3 =5 x^2 +y^2 =3 |

|
| if z = − 27, find all the root of z in complex plain |
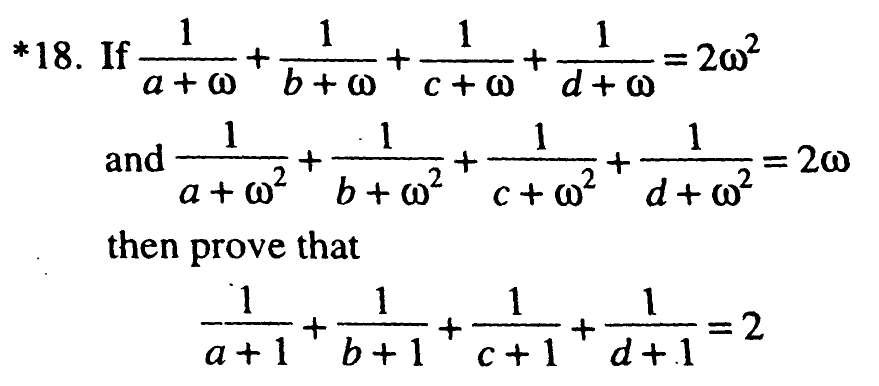
|
| simplify Σ_(k=0) ^n (C_n ^k /(k+1)) |
Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 |