
Question and Answers Forum
AlgebraQuestion and Answers: Page 331




Pg 326 Pg 327 Pg 328 Pg 329 Pg 330 Pg 331 Pg 332 Pg 333 Pg 334 Pg 335
|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 331 |
| find the sum s_0 = C_n ^o +C_n ^4 +C_n ^8 +... s_1 = C_n ^1 +C_n ^5 +C_n ^9 +.... s_3 = C_n ^2 +C_n ^6 + C_n ^(10) +.... |
| let give α ∈]−π ,π[ 1)prove that sin^2 α −2(1+cosα) =−4cos^4 ((α/2)) 2)solve inside C z^2 −2z sinα +2(1+cosα)=0 find the module and arg of the roots. |
| let θ∈[0,π] and Z=1+cosθ +isinθ Z^′ =cosθ +(1+sinθ)i find ∣ZZ^′ ∣ arg(ZZ^′ ) ∣(Z/Z^′ )∣ , arg((Z/Z^, )) , ∣Z−Z^, ∣ and arg(Z−Z^, ). |
| solve inside C z^6 = (z^− )^2 . |
| 1) solve x^5 =1 2) if x_i are roots of this equation prove that Σ_i x_i =0 3)prove that cos(((2π)/5)) +cos(((4π)/5)) =−(1/2) 4)calculate cos(((4π)/5)) interms cos(((2π)/5)) then find its values. |
| 1) solve inside C z^4 =6 2)sove inside C (((z+i)/(z−i)))^3 +(((z+i)/(z−i)))^2 +(((z+i)/(z−i))) +1=0 |
| factorize p(x)=(1+ix)^n −e^(inθ) wth θ∈R. |
| let give x_0 =0 ,y_0 =1 and {_(y_n =x_(n−1) +y_(n−1) ) ^(x_n =x_(n−1) −y_(n−1) ) for n≥1 let z_n =x_n +i y_n ∀n∈N 1)calculate z_0 ,z_1 and z_2 2)prove that ∀n∈N^ ,n≥1 z_n =(1+i)z_(n−1) find z_n then find the expression of x_n and y_n 3)let put S_n =z_0 +z_1 +....z_n s_n =x_0 +x_1 +...+x_n s_n ^′ =y_0 +y_1 +...+y_n find those sum interms of n. |
| 1) solve inside C z^(12) =1 and give the solution at form r e^(iθ) 2)calculate 1+u +u^2 +... +u^n then find the solution of z∈C z^8 +z^4 +1=0 |

|

|
| Number of positive integers x for which f(x)=x^3 −8x^2 +20x−13 is a prime number are ? |

|
|

|
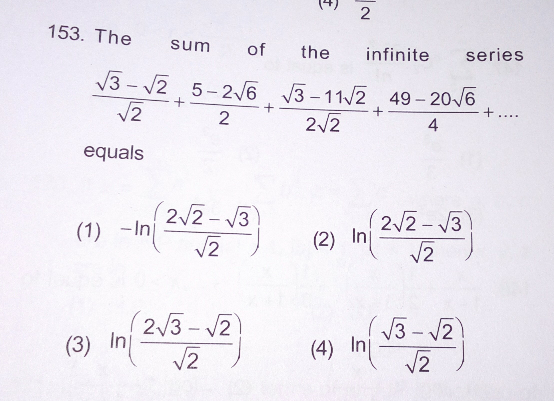
|
| S= 3(1!)−4(2!)+5(3!)−6(4!)+.... .....−(2008)(2006!)+2007! Find value of S. |
| x^7 +x^6 +x^5 +x^4 +x^3 +x^2 +x+1=0 Σ_(k=1) ^7 [ℜ(x_k )]^2 = ? x_k = k^( th) root of the equation ℜ(x_k ) = real part of the root |
| let U_n ={z∈C/z^n =1} simlify A_n = Σ_(α∈U_n ) (x+α)^n and B_n =Σ_(α∈ U_n ) (x−α)^n . |
| let p(x)= (x−1)^n −x^n +1 with n integr find n in ordre that p(x) have a double root. |
| decompose inside R[x] p(x)=x^(2n+1) −1 then find Π_(k=1) ^n sin( ((kπ)/(2n+1))) . |
| prove that ∀p ∈N it exist one polynomial Q_(2p) / sin(2p+1)θ=sin^(2p+1) θ Q_(2p) (cotanθ) and degQ_(2p) =2p 2) prove that Π_(k=1) ^p tan(((kπ)/(2p+1)))=(√(2p+1)) . |
| let (u_n ) / u_1 =1−i and ∀p∈{2,3,...n} u_p =u_(p−1) j with j=e^(i((2π)/3)) 1)verify that u_1 +u_2 +u_3 =0 2)prove that ∀p∈ {4,5,...,n} u_p =u_(p−3) 3)find the value of S_n =Σ_(i=1) ^n u_i 4)calculate α_n = Σ_(p=0) ^(n−1) cos(−(π/4) +((2pπ)/3)) and β_n = Σ_(p=0) ^(n−1) sin(−(π/4) +((2pπ)/3)). |
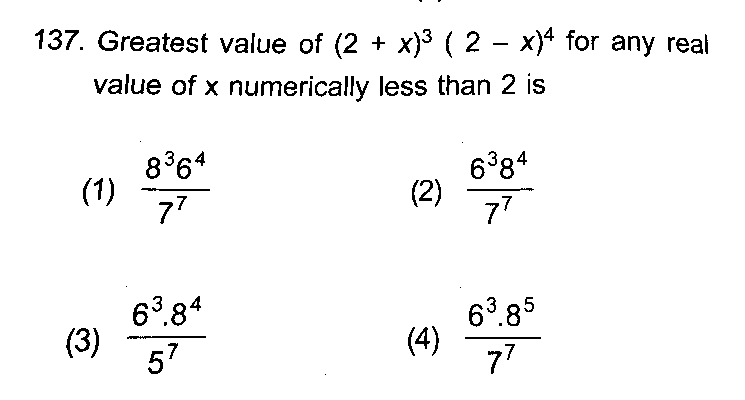
|
| let w_k =e^(i((2kπ)/n)) find A= Π_(k=0) ^(n−1) (a +bw_k ). |
| decompose inside C(x) F= (1/((x−1)(x^n −1))) . |
Pg 326 Pg 327 Pg 328 Pg 329 Pg 330 Pg 331 Pg 332 Pg 333 Pg 334 Pg 335 |