
Question and Answers Forum
AlgebraQuestion and Answers: Page 81





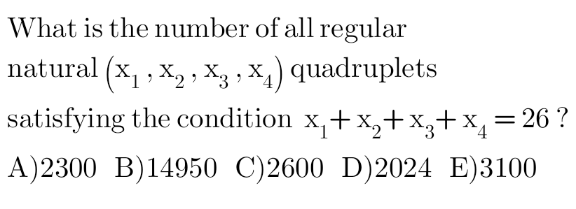


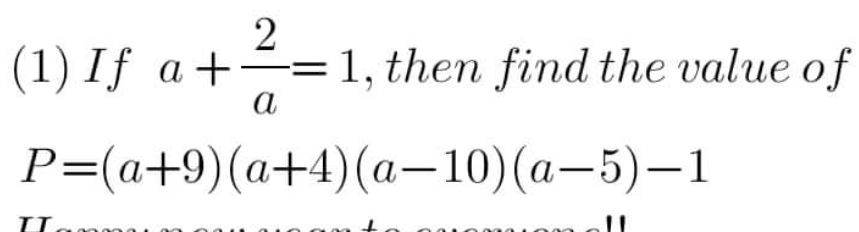

|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 81 |
| α , β are roots of , x^( 2) −x−1=0 ( α > β ) and , t_( n) = ((α^( n) − β^( n) )/(α−β)) ( n ∈ N ), if , b_1 =1 , b_( n) = t_( n−1) +t_( n−2) ( n ≥2 ) find the value of S = Σ_(n=1) ^∞ (( b_( n) )/(10^( n) )) =? |
| x^( 2) − 3x +1=0 α , β are roots : ( α^( 3) +(1/β) )^( 3) + ( β^^( 3) +(1/α) )^( 3) = ? |

|

|
| Solve for real numbers: sinx (√(1 − sin^2 x)) = 1 + cosy (√(1 − cos^2 y)) |
| solve { ((x^2 −xy+y^2 =16)),((y^2 −yz+z^2 =25)),((z^2 −zx+x^2 =49)) :} |

|

|
| Resoudre dans Z^+ (√a) +(√b) =z (a,b,z)∈N^3 a,b ? |
| Suppose that the sum of the square of complex numbers x or y is 7 , and the sum of their cubes is 10. Find the largest true value of the sum x+y that satisfies these conditions. A)4 B)5 C)6 D)7 E)8 |
| Resoudre dans Z^+ x+y+(√(xy)) =39 |
| If a, b>0 such that 2a+b=2, then find the minimum value of: 1) (4a^2 +1)(b^2 +1) 2) ((2a^2 −b+4)/(a+1))+((b^2 −2a−2)/(b+4)) |

|
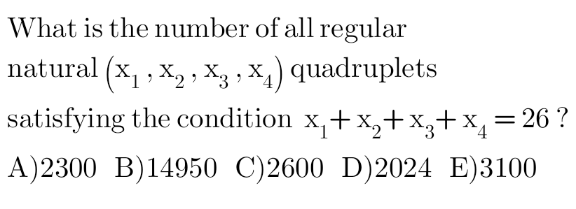
|

|
| If A = 20° and B = 25° Find (1 + tanA)(1 + tanB) |
| Choose 4 random points in a sphere to form a tetrahedron inside the sphere. What is the probability that this tetrahedron contain the centre point of the sphere? |
| solve in R^3 { ((x+(1/y)=3)),((y+(1/z)=4)),((z+(1/x)=5)) :} |
| If a − (4/( (√a))) = 17 Find a − 4 (√a) = ? |
| (2a−b)b+(5/(3a))−7b^2 +3a=0 Evaluer b en fonction de a |
| U_n = ((((−4)^(n+1) −1)/(1−(−4)^n )))U_(n−1) with U_0 =1 find U_(n ) in terms of n (question Q173132 reposted) |

|
| f(x)=((a^x +b^x +c^x )/x) with a+b+c=0 prove f(7)=f(5)×f(2) |
| if: f(x) = x^2 + 2x find x: f(f(f(x + 2))) = 99 999 999 |
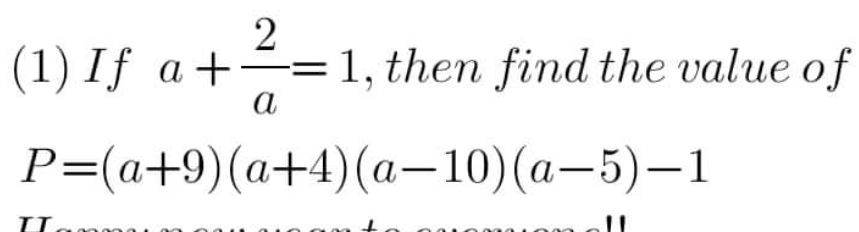
|

|