
Question and Answers Forum
AlgebraQuestion and Answers: Page 83


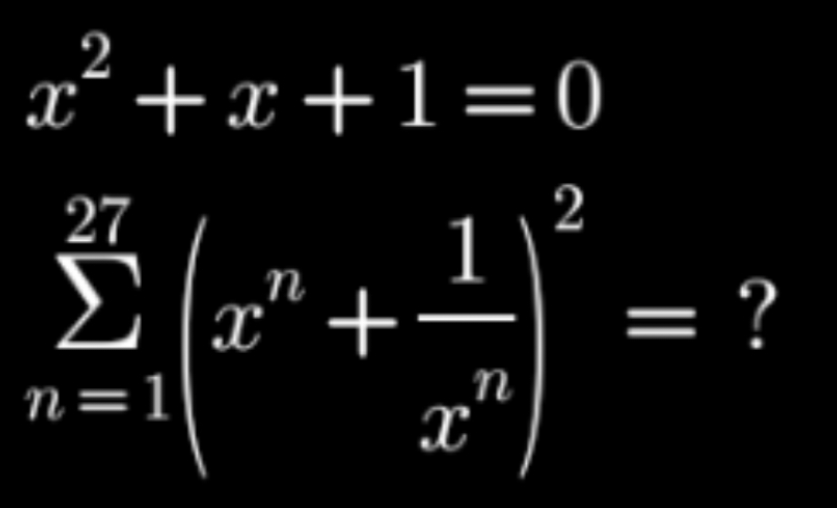



|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 83 |

|
| Among the natural numbers not greater than 22 , the probability that the modulus of the difference of any two of the 3 randomly selected numbers is greater than 5 is equal to which of the following? a)15/22 b)1/7 c)1/22 d)1 |
| ((3n^5 + 4n^4 − 7n^3 + 5n^2 − 5)/(n + 1)) There can be no residue: a)0 b)2 c)4 d)5 e)9 |
| a>0 , b>0 { (((x−1)^2 + (y−7)^2 = a^2 )),(((x−2)^2 + (y−3)^2 = b^2 )) :} Find: (a+b)_(min) = ? |
| { (((√(x/y)) +(√(y/z)) +(√(z/x)) = 3)),(((√(y/x)) +(√(z/y)) +(√(x/z)) = 3)),(((√(xyz)) = 1)) :} |
| 6 of the 23 given points in the plane lie on a circle. Let n be the number of circles passing through at least 3 of these points. What is the maximum number of n? |
| Find: 2003∙2005^3 −2004∙2002^3 |
| Given three point.Find the for the plane through the point P(0,1,0) Q(3,1,4) R(−1,0,1) |
| For the function f(x)= { ((x^2 −3 if x<4)),(((x^2 /(x+4)) if x≥4)) :} Find (i) lim_(x→−4) f(x) ii)lim_(x→+4) f(x) |
| For the function f(x)= { ((1−x^2 if x< 2)),((2x+1 if x≥2)) :} Find (i)lim_(x→^− 2) f(x) (ii) lim_(x→2^+ ) f(x) |
| Find (a)lim_(x→∞) ((3x+2)/(x^2 −x+1)) (b)lim_(x→∞) ((√(x^2 −1))/(2x+1)) (c)lim_(x→5) (((√(3x+1)) −4)/(x−5)) |
| Find: 3 − (2/(3 − (2/(3 − (2/(...)))))) = ? |
| Find the equation of the line which is tangent to the parabola y^2 =12x and forms an angle of 45° with the line y=3x−4. |
| Find the coefficient of x^(11) in (2x^2 +x−3)^6 . |
| In △ABC the following relationship holds: (m_b /b) + (m_c /c) ≤ (a/(2r)) ≤ (n_b /h_b ) + (n_c /h_c ) |
| I−Incenter in △ABC A(2,2) , B(6,4) , C(4,8) , M(8,6) Find: MI = ? |

|
| Simplify ^3 (√(56^3 (√(4 )) − 157^3 (√9) + 130^3 (√6) )) into a compound surd. |
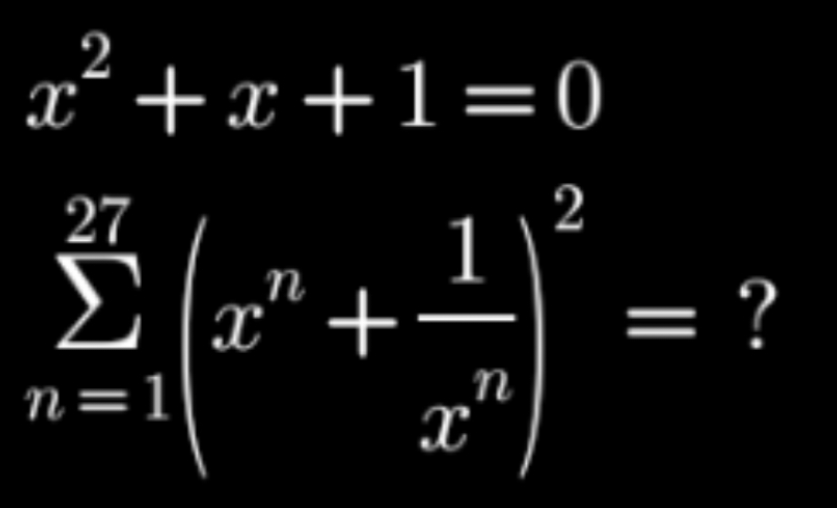
|

|

|

|
| Find the equation of the line which passes through the point (3, 5) and is tangent to the circle (x−1)^2 +(y−1)^2 =4 |
| Find: (√(12−2(√(35)))) − (√(10−2(√(21)))) = ? |
| Q f(x)=a^x +b^x g(x)=((f(x))/(f(x−2))) g(3)=? |
| (√(m^2 −4m+4)) + ((m−2n+8))^(1/4) = 0 n = ? |