
Question and Answers Forum
AlgebraQuestion and Answers: Page 97

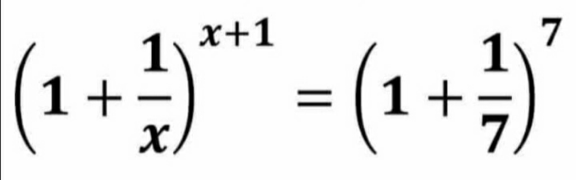




Pg 92 Pg 93 Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101
|
Question and Answers Forum |
AlgebraQuestion and Answers: Page 97 |
| △ABC, sinA=cosB=tanC find the value of cos^3 A+cos^2 A−cosA. |
| z∈C, ((z−3i)/(z+i))∈R^− , ((z−3)/(z+1))∈I find z. |

|
| L(E) est l′algebre des endomorphisme continus d′un espace de Banach E, muni de la norme d′application lineaire ; GL(E) est le sous ensemble des elements inversibles de L(E) a)Montrer que GL(E) est ouvert dans L(E) b)montrer que l′application ∅:GL(E)→GL(E) u→u^(−1) =∅(u) est continu dans GL(E) c)montrer que ∅ est differentiable dans GL(E) dt calculer d∅ |
| solve for x,y,z with x+y+z=x^2 +y^2 +z^2 =x^3 +y^3 +z^3 =5 |
| x^2 +x=1 ((x^5 +8)/(x+1))=? |
| If , α , β , γ ∈ ( 0 , 1 ) , then prove that : (√((1−^ α ).(1−^ β ). (1−^ γ ))) +(√(α^ .β^ .γ^ )) < 1 |
| Suppose a^3 +b^3 +c^3 =a^2 +b^2 +c^2 =a+b+c Prove that abc=0 |
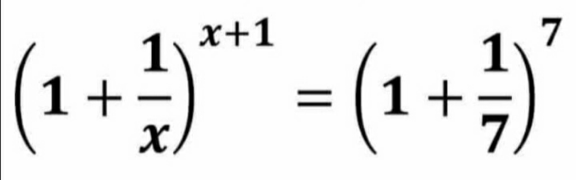
|

|
| x^3 +(1/x^3 ) = 1 ⇒(([x^5 +(1/x^5 )]^3 −1)/(x^5 +(1/x^5 ))) =? |
| Find the constant term in the expansion of the expression (2+3x)^3 ((1/x)−4)^4 |
| show that 1+2+3+4+................ ∞ = ((−1)/8) |
|
| In △ABC the following relationship holds: Σ_(cyc) (a^2 /(b^2 + c^2 )) + 4 Π_(cyc) cos A ≤ 2 |
| p(x)=2x^2 +(√(4x^2 )) pq=4 and p+q=2 faind p^a_2 +q^a_1 =? |
| (2+(1/4)x^2 )^5 (2−(1/3)x^2 )^5 find coefficient x^2 |

|
| coeffisien x^(2 ) from (2+(1/4)x^2 )^5 (1−4x)^5 |
| Let a, b, c >0. If ((a−b)/b)>7, ((b+c)/c)<8, Find min(a+b+c) |
| Proof that : ∄n∈Z, n^2 +1≡0(mod 4) |
| coeff of x^2 from [6+8x−(3/2)x^2 ]^5 |

|
| solve for x (1+(1/x))^(x+1) =(1+(1/6))^6 show working |

|
| Find how many distinct integers are there in this sequence: ⌊((1^2 +1)/(100))⌋, ⌊((2^2 +2)/(100))⌋, ⌊((3^2 +3)/(100))⌋, ..., ⌊((100^2 +100)/(100))⌋ where ⌊x⌋ is the greatest integer that is less than or equal to x |
Pg 92 Pg 93 Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 |