
Question and Answers Forum
AllQuestion and Answers: Page 1025




Pg 1020 Pg 1021 Pg 1022 Pg 1023 Pg 1024 Pg 1025 Pg 1026 Pg 1027 Pg 1028 Pg 1029
|
Question and Answers Forum |
AllQuestion and Answers: Page 1025 |

|
| the sum of all x values (x^2 −6x+9)^((x−3)/(x−1)) = (x−3)^((x−4)) |
| Find the gcd(n−1,n+1) |

|
| Find all continuous real function f such that f(ln(x+y))=f(sin(xy))+f(cos(y/x)) for all x,y∈R^+ . |
| If (f(x).g(x))′ = f(x)′ . g(x)′ find the function of f(x) . |
| calculate U_n =∫_([(1/n),n[^2 ) (x^2 −y^2 )e^(−x^2 −y^2 ) dxdy and lim_(n→+∞) U_n |
| find ∫∫_([0,1]^2 ) ln(x^2 +3y^2 ) e^(−x^2 −3y^2 ) dxdy |
| find lim_(x→0) ((arctan(x−sinx)−arctan(1−cosx))/x^2 ) |
| calculate ∫_(−∞) ^(+∞) ((cos(2x))/((x^2 −4i)^3 ))dx (i=(√(−1))) |
| calculate ∫_(−∞) ^(+∞) (dx/((x^2 −ix +1)^2 )) (i=(√(−1))) |
| Given lim_(x→0) (f(x)+(1/(f(x)))) = 2 , find the value of lim_(x→0) f(x). |
| If 2f(x) + f((1/x)) = 3x what is f(x) |
| The product of the four terms of an increasing arithmetic progression is a, their sum is b, and the sum of their reciprocal is c. Suppose that a,b,c form a geometric progression whose product is 8000, find the sum of the first and fourth term. |
| Which of the following is not a factor of x^6 −56x+55 A. x−1 B. x^2 −x+5 C. x^3 +2x^2 −2x−11 D. x^4 +x^3 +4x^2 −9x+11 E. x^5 +x^4 +x^3 +x^2 +x−55 Please show all workings clearly. Thanks. |
| Prove that x^5 −3x^4 −17x^3 −x^2 −3x+17 cannot be factorized completely over the set of polynomials with integral coefficients. |
| Let t be a root of x^3 −3x+1=0, if ((t^2 +pt+1)/(t^2 −t+1)) can be written as t+c for some p,c ∈ Z, then p−c equals? |
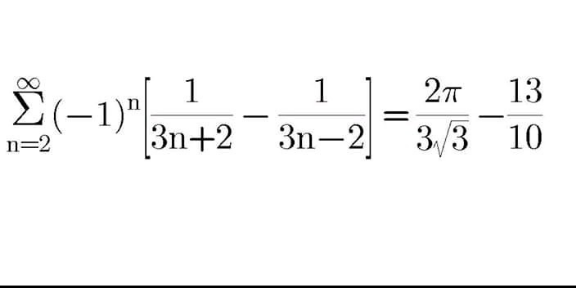
|
| if W represents the Runesky determinant of the two independent solutions linearly (y_1 ,y_2 )of the equation y^(′′) +p(x)y^′ +Q(x)=0 then demonstrate that W satisfies the differential equation (W^( ′) +p(x)W=0) and solve this equation to qet W ? help me sir please |
| The identity 2[16a^4 +81b^4 +c^4 ]=[4a^2 +9b^2 +c^2 ]^2 cannot result from which of the following equations? A. 6b=4a+2c B. 6a=9b+3c C. 6b=−4a+2c D.c= −2a−3b E. 6c=2b+3a |
| prove to ealier problem of ∫_0 ^1 ∫_0 ^1 ((tanh^(−1) ((x)^(1/4) )tanh^(−1) ((y)^(1/4) ))/(x(√y)))dxdy=π^2 solution let I=∫_0 ^1 ((tanh^(−1) ((x)^(1/4) ))/x)dx∫_0 ^1 ((tanh^(−1) ((y)^(1/4) ))/(√y))dy=A.B let m=x^(1/4) and dx=4m^3 A=∫_0 ^1 ((tanh^(−1) (m))/m^4 )×4m^3 dm=4∫_0 ^1 ((tanh^(−1) (m))/m)dm but series of tanh^(−1) (m)=Σ_(k=0) ^∞ (m^(2k+1) /(2k+1)) A=4Σ_(k=0) ^∞ (1/(2k+1))∫_0 ^1 (m^(2k+1) /m)dm=4Σ_(k=o) ^∞ (1/(2k+1))∫_0 ^1 m^(2k) dm A=4Σ_(k=0) ^∞ (1/((2k+1)^2 ))=4×(1/2)Σ_(k=−∞) ^∞ (1/((2k+1)^2 )) recall that Σ_(n=−∞) ^∞ (1/((an+1)^m ))=−(π/((a)^m ))lim_(z→−(1/a) ) (1/((m−1)!))(d^((m−1)) /dz^((m−1)) )[cot(πz)] ∵A=2[−(π/((2)^2 ))lim_(z→−(1/2)) (1/((2−1)!))(d/dz)[cot(πz)] A=−(π/2)lim_(z→−(1/2)) [−πcosec^2 (−(π/2))]=(π^2 /2).....(1) then B=∫_0 ^1 ((tanh^(−1) ((y)^(1/4) ))/(√y))dy let n=y^(1/4) and dy=4n^3 B=∫_0 ^1 ((tanh^(−1) (n))/n^2 )×4n^3 dn=4∫_0 ^1 ntanh^(−1) (n)dn B=4Σ_(k=0) ^∞ (1/(2k+1))∫_0 ^1 n^(2k+2) dn=4Σ_(k=0) ^∞ (1/((2k+1)(2k+3))) B=4×(1/2)Σ_(k=0) ^∞ ((1/(2k+1))−(1/(2k+3))) B=2lim_(k→∞) (1−(1/3)+(1/3)−(1/5)+(1/5).......+(1/(2k+1)))=2.....(2) the series is telescoping but I=A×B=(π^2 /2)×2=π^2 ..............(3) ∫_0 ^1 ∫_0 ^1 ((tanh^(−1) ((x)^(1/4) )tanh^(−1) ((y)^(1/4) ))/(x(√y)))dxdy=π^2 Q.E.D by mathdave(28/08/2020) |

|
| If P(x) is a polynomial whose sum of coefficients is 3 and P(x) can be factorised into two polynomials Q(x),R(x) with integer coefficients, the sum of the coefficients Q(x)^2 +R(x)^2 is |

|
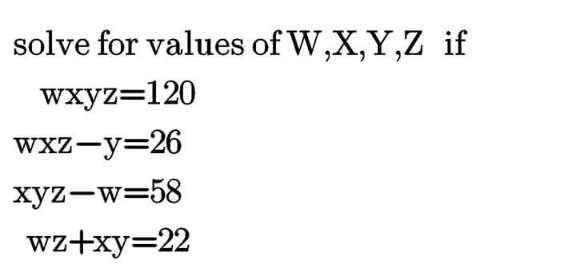
|
| Let f(x)=∣x−2∣+∣x−4∣−∣2x−6∣, for 2≤x≤8. The sum of the largest and smallest values of f(x) is |
Pg 1020 Pg 1021 Pg 1022 Pg 1023 Pg 1024 Pg 1025 Pg 1026 Pg 1027 Pg 1028 Pg 1029 |