
Question and Answers Forum
AllQuestion and Answers: Page 107

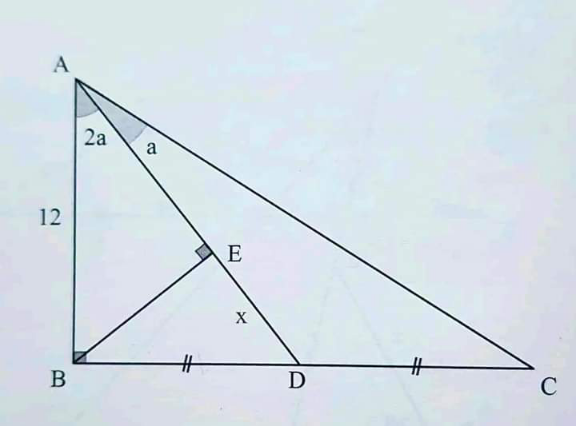




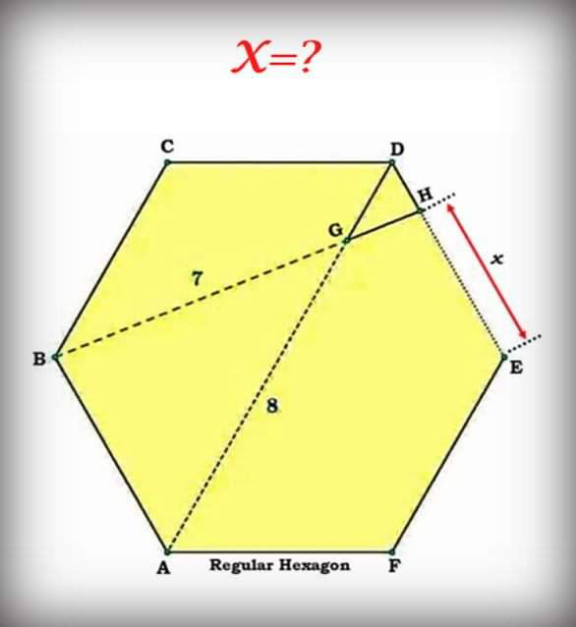

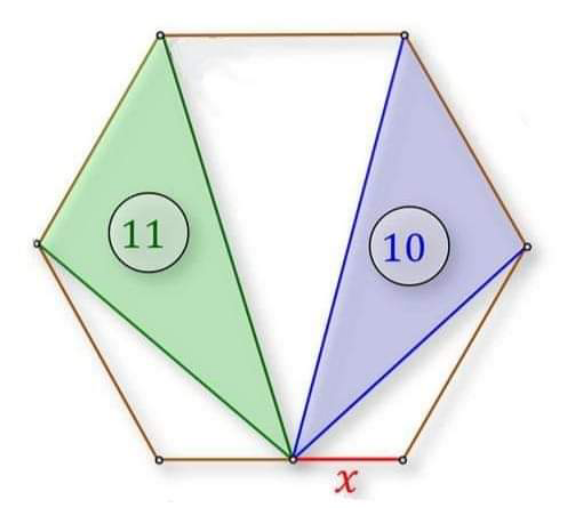


Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111
|
Question and Answers Forum |
AllQuestion and Answers: Page 107 |
| Resuelve la siguiente integral ∫ ((sin (t))/( ((sin^7 (t)∙cos^5 (t)))^(1/4) )) dt |

|
| If a>b>0 and 4a^2 + b^2 = 4ab Find: ((a − b)/(a + b)) = ? |
| If (a^2 /(12)) − 5b^3 = −30 Find: (2/(45)) a^2 − (8/3) b^3 = ? |
| If 4^p = 5 Find: 2^(3p) = ? |
| If asinθ = bcosθ = ((2ctanθ)/(1 − tan^2 θ)) then prove that (a^2 − b^2 )^2 = 4c^2 (a^2 + b^2 ). |

|
| if f(x)=(√(x−x^2 )) then f^(−1) (x)=? |

|

|
| solve the first order differential equation: xdy − ydx = (xy)^(1/2) dx |

|

|
| If tan^2 θ = 1 − x^2 then prove that secθ + tan^3 θcosecθ = (√((2 − x^2 )^3 )) . |
| let f:[0,∞)→R be a continuous function if lim_(n→∞ ) ∫_0 ^1 f(x+n)dx = 2 then lim_(n→∞) f(nx) = ? |

|
| If cos𝛂 = (3/5) (0<𝛂<(𝛑/2)) Find: ((tan^2 (45° + (𝛂/2)))/3) = ? |
| If tanpθ = ptanθ then prove that ((sin^2 pθ)/(sin^2 θ)) = (p^2 /(1 + (p^2 − 1)sin^2 θ)) . |

|

|

|
| find S=1+Σ_ℓ (((−)^ℓ )/ℓ)((1/ℓ)−(1/(ℓ+1))) , ℓ∈[1,∞) 1+Σ_ℓ (((−)^ℓ )/ℓ)((1/ℓ)−(1/(ℓ+1))) 1−(1−(1/2))+(1/2)((1/2)−(1/3))−(1/3)((1/3)−(1/4))+(1/4)((1/4)−(1/5))−...... |
| Find: ∫_(−3) ^( −2) (∣x∣ + ∣x − 4∣) dx = ? |
| Number series: a_3 = 2a + b − 6 a_9 = a + b + 5 a_(15) = 3a + b − 7 Find: a = ? |

|
| If 0<a<1 Compare: (1/(a−1)) , (a/(a−1)) , (1/(1−a)) , (a/(1−a)) , (a/(2a)) |
Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 |