
Question and Answers Forum
AllQuestion and Answers: Page 115
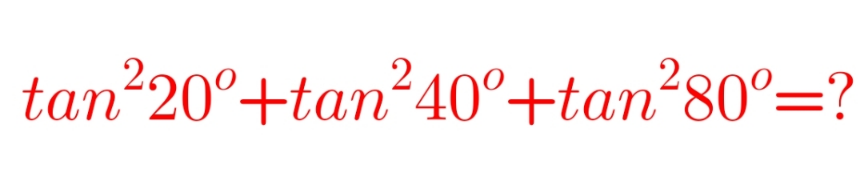









Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119
|
Question and Answers Forum |
AllQuestion and Answers: Page 115 |
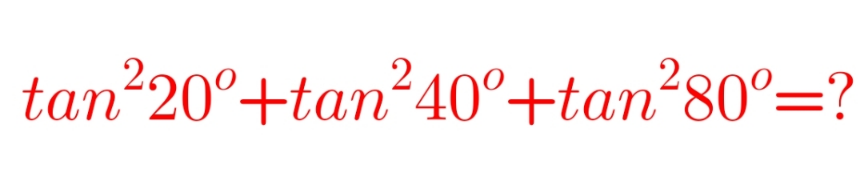
|
| ((exercice )/) prouver ∫_0 ^𝛑 ∫_0 ^x sin((x^2 /𝛑))dxdy=𝛑 ...............prof cedric junior........... |
| If , f(x) = { (( 2^(2x) − log_3 ( x+3 ) ; x ≥5)),(( f (1+ x ) −4 ; x < 5)) :} ⇒ f (0 )= ? |

|
| ∫((x−x^2 ))^(1/3) dx |
| f(x) = x^3 − 16x^2 − 57x +1 f(a)= 0 f(b)=0 f(c)=0 (a)^(1/5) + ((b ))^(1/5) + ((c ))^(1/5) = ? |

|
| For z = a − bi If (∣z∣ − z)∙(∣z∣ + z^(−) ) = 4bi Find ∣z∣ = ? |
| How Can derive LambertW(z) in the Form of integral??? W(z)=(1/π)∫_0 ^( π) ln(1+((z∙sin(t))/t)e^(t∙cot(t)) )dt , z∈[−(1/e),∞) Or Similar to the example.LambertW(z) How other Functions can be Derived in Integral Form |
| find the value of I=∫_0 ^(+∞) ln(1+e^(−x) )dx nowing that Σ_(n=1) ^(+∞) (1/n^2 )=(π^2 /6) |
| how to convert 31230 in base 60? pls help |
| lim_(n→∞) n^(−3/2) [(n+1)^((n+1)) (n+2)^((n+2)) ...(2n)^(2n) ]^(1/n^2 ) = ? |

|
| lim_(n→∞) n^(−3/2) [(n+1)^((n+1)) (n+2)^((n+2)) ...(2n)^(2n) ]^(1/n^2 ) = ? |
| If a = (1/2^2 ) + (1/3^2 ) + ... + (1/(100^2 )) b = 0,99 Prove that: a < b |
| In a regular pentagon PQRST , PR intersects QS at O. Calculate ROS? |

|

|

|

|

|
| solve for x∈C 3^(2ix) −3^(ix) 2+5=0 |
| solve for x x^2 −10⌊x⌋+((57)/4)=0 |
| solve for x≠y∧y≠z∧z≠x (exact solutions required) (√((−3+4i)x))=y (√((−3+4i)y))=z (√((−3+4i)z))=x |

|
| Prove that: (1/3^3 ) + (1/4^3 ) + ... + (1/n^3 ) < (1/(12)) |
Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 |