
Question and Answers Forum
AllQuestion and Answers: Page 1161
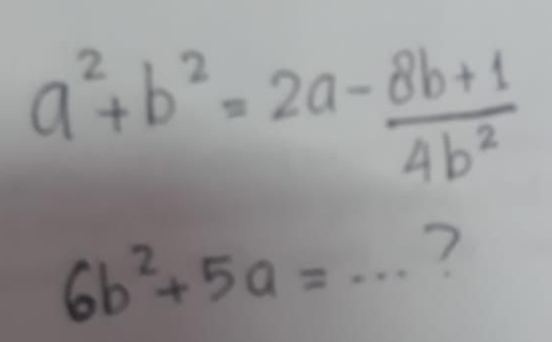


Pg 1156 Pg 1157 Pg 1158 Pg 1159 Pg 1160 Pg 1161 Pg 1162 Pg 1163 Pg 1164 Pg 1165
|
Question and Answers Forum |
AllQuestion and Answers: Page 1161 |
| (xy+sin y)dx+(0.5x^2 +xcos y)dy=o |
| y^′ −y.tan x+y^2 cos x=0 |

|
| ∫t^2 /(1+t^2 )^2 dx= |
| prove that the equation of the normal to the rectangular hyperbola xy = c^2 at the point P(ct, c/t) is t^3 x −ty = c(t^4 −1). the normal to P on the hyperbola meets the x−axis at Q and the tangent to P meets the yaxis at R. show that the locus of the midpoint oc QR, as P varies is 2c^2 xy + y^4 = c^4 . |
| ∫(log x/x^2 )dx= |
| 1\Calculate f_x (2,3) if f(x,y)=x^2 +y^2 2\Calculate df(x,y) for x=1, y=0, dx=(1/2) and dy=(1/4) if f(x,y)=(√(x^2 +y^2 )) |
| Differentiate completely; 1\ f(x,y)=x^2 +xy^2 +siny 2\ f(x,y)=e^(x^2 +y^2 ) 3\ f(x,y,z)=tan(3x−y)+6^(y+2) |
| Q. Prove by mathematical induction that Σ_(r=1) ^n (4r + 5) = 2n^2 + 7n |
| ∫1/(1+x^2 )^2 |
| ∫1/1+x2 |
| Solve: 3x^(x + 1) − 3x^(x − 1) = 8 |
| ∫ (sin x+2cos x)^3 dx |
| If f a function such that f(a).f(b)−f(a+b)=a+b. find the value of f(2019) |
| solve for x,y >0 2x⌊y⌋ = 2020 3y⌊x⌋ = 2021 |
| Solve by using change the conistant megbod 4y^(′′) +y=((x^2 −1)/(x(√x)))? |
| what is the value of coefficient of x^9 in expansion (1+x)(1+x^2 ) (1+x^3 )(1+x^4 )×...×(1+x^(100) ) ? |
| To tinkutara I have forget my old password and has to create a new one. Is there any way to retrive my old account. |
| what is the coefficient of x^5 in the expansion (1+x^2 )(1+x)^4 |
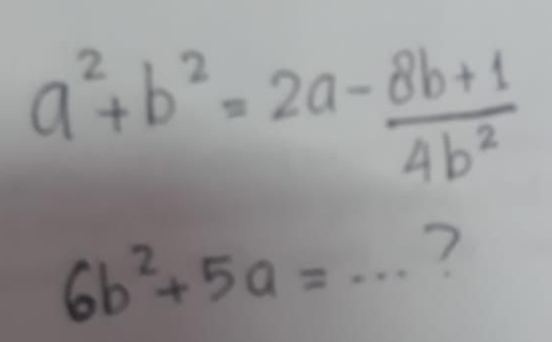
|

|

|
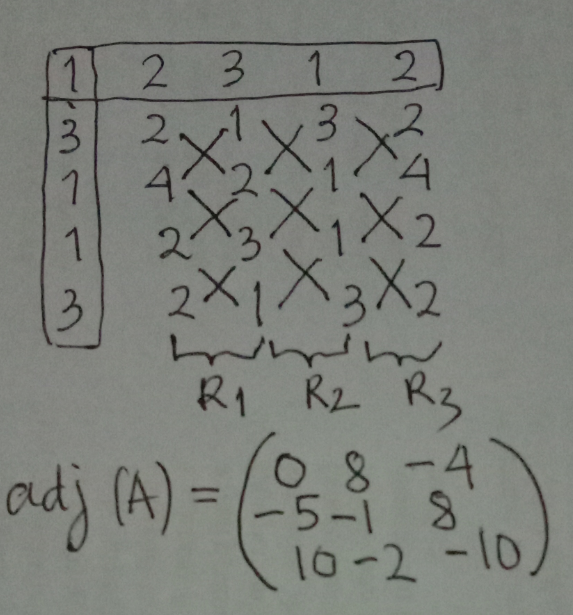
| let A= (((1 2 3)),((3 2 1)) ) ∈M_3 (C) (1 4 2 ) 1) find A^(−1) if A inversible 2) calculate A^n 3)find cosA and sinA 4) is cos^2 A +sin^2 A =I ? |
| let A = (((1 −1)),((1 1)) ) 1) calculate A^(−1) and A^(−2) 2) calculate A^n 3) find e^A and e^(−A) |
| let p(x)=((x^n (4−2x)^n )/(n!)) 1) prove that p^((k)) (0)=p^((k)) (2)=0 for all k∈[1,n−1] 2) prove that ∀m∈N p^((m)) (0) and p^((m)) (2) are integrs |
| ∫((1+x^6 )/(1+x^8 ))dx |
Pg 1156 Pg 1157 Pg 1158 Pg 1159 Pg 1160 Pg 1161 Pg 1162 Pg 1163 Pg 1164 Pg 1165 |