
Question and Answers Forum
AllQuestion and Answers: Page 1164





Pg 1159 Pg 1160 Pg 1161 Pg 1162 Pg 1163 Pg 1164 Pg 1165 Pg 1166 Pg 1167 Pg 1168
|
Question and Answers Forum |
AllQuestion and Answers: Page 1164 |
| ((s(t+Δt)−s(t))/(Δt)) |

|

|
| ∫(√(tan x)) dx=? |
| ∫((x((x−a))^(1/3) )/((x−b))^(1/3) )dx=? ∫(((x−a))^(1/3) /(x((x−b))^(1/3) ))dx=? |
| { ((x+y = 10)),(((x)^(1/(3 )) + (y)^(1/(3 )) = (5/2) ((xy))^(1/(6 )) )) :} find x &y?? |
| ∫ (dx/(p+(√(qx+r)))) |

|
| solve cosz =e^z zfrom C |
| There is a moving point P in a triangle ABC of which sides are a,b,c and a>b>c find the minimum and maximum of AP+BP+CP |
| ∫ (dx/((x+(√(1+x^2 )))^2 )) = |
| f(x) is a continuous function forall real values of x and satisfies∫_0 ^x f(t).dt=∫_x ^1 t^2 .f(t).dt+(x^(16) /8)+(x^6 /3)+A Find A? |
| lim_(x→1) ( (1/(x−1)) − (x/(ln x)) ) = ... ( Without L′ Hospital ) |

|
| ∫(√(cotx))dx |
| P is the point representing the complex number z = r( cos θ + i sin θ) in an argand diagram such that ∣z−a∣∣z + a∣ = a^2 . Show that P moves on the curve whose equation is r^2 =2a^2 cos2θ. sketch the curve r^2 = 2a^2 cos 2θ , showing clearly the tangents at the pole. |
| 3.(a) Find the complex number z which satisfy the equation z^3 = 8i , giving your answer in the form a + bi where a and b are real. |
| ∫_2 ^4 ((3x−2)/(x^2 −4)) dx = ? |
| Given the function f defined by f(x) = ((∣x−2∣)/(1−∣x∣)) (i) state the domain of f. (ii) show that f(x) = { ((((2−x)/(1+x)) , x < 0)),((((2−x)/(1−x)), 0 ≤ x < 2)),((((x−2)/(1−x)) , x ≥ 2)) :} (iii) Investigate the continuity of f at x = 2. |

|
| Given a function H(x) = ∣sin x+cos x∣ + (√2) cos x with x ∈ [ 0, 2π ] find H(x)_(max) and H(x)_(min) |
| 20+a=a cosh(((75)/a)) a=? |
| prove that ∫_0 ^∞ ((sin^(2n) (x))/x^2 )d=∫_0 ^∞ ((sin^(2n−1) (x))/x)dx |
| Find ∫_( 1) ^( ∞) ((sin^2 x)/x^2 ) dx |
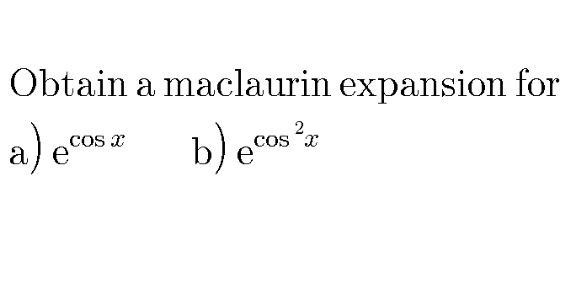
|
| LCM(a,(3/5)a)=3a ∧ HCF(a,(3/5)a)=(1/5)a a=? |
Pg 1159 Pg 1160 Pg 1161 Pg 1162 Pg 1163 Pg 1164 Pg 1165 Pg 1166 Pg 1167 Pg 1168 |