
Question and Answers Forum
AllQuestion and Answers: Page 1330








Pg 1325 Pg 1326 Pg 1327 Pg 1328 Pg 1329 Pg 1330 Pg 1331 Pg 1332 Pg 1333 Pg 1334
|
Question and Answers Forum |
AllQuestion and Answers: Page 1330 |

|
| prove that for z ∈C arctanz =(1/(2i))ln(((1+iz)/(1−iz))) |
| let 0<a<1 calculate ∫_0 ^∞ ((ln(t)t^(a−1) )/(1+t))dt and ∫_0 ^∞ ((ln^2 (t)t^(a−1) )/(1+t))dt |

|
| calculate Σ_(n=1) ^∞ (n^4 +2n^2 −3)(x^n /(n!)) in case of convergence. |
| find the sum of Σ_(n=0) ^∞ (n^2 −3n+1)e^(−n) |
| calculate A_n =∫_0 ^∞ ((1+x^n )/(2+x^(2n) ))dx and J_n =∫_0 ^∞ ((2+x^(3n) )/(5+x^(7n) ))dx with n integr natural not 0 |
| find the polynom T_n wich verify T_n (cosθ)=cos(nθ) ∀n integr ∀θ real 1) find T_0 ,T_1 and T_2 and prove that T_(n+2) =2x T_(n+1) −T_n 3) find deg(T_n ) and T_n (1) ,T_n (−1) 4) find T^′ (cosθ) for 0<θ<π and prove that (1−x^2 )T_n ′′−xT′_n +n^2 T_n =0 5) find roots of T_n and decompose T_n inside R[x] 6) find the value of Π_(k=0) ^(n−1) cos((((2k+1)π)/(2n))) |
| calculate f(x)=∫_0 ^π ln(x^2 −2xcosθ +1)dθ with x real. |
| find the coefficient a_k of term x^k in Π_(r=1) ^n (1+x^r ) with 0≤k≤((n(n+1))/2) example: n=100, k=50 |
| lim (0/∞) =^(?) 0 ? lim (∞/0) =^(?) ∞ ? |

|

|

|

|
| ∫((2x^2 −1+2x(√(x^2 −1)))/(x^2 −x+(x−1)(√(x^2 −1))))dx=? ∫(dx/(x(√(x+1))(√((1−x)^3 ))))=? |
| if lim_(x→0^+ ) f(x)=+∞ lim_(x→0^− ) f(x)=+∞ then lim_(x→0) f(x)=+∞ or lim_(x→0) f(x)=not exist |

|
| find x and y: { ((2x^y −x^(−y) =1)),((log_2 y=(√x))) :} |
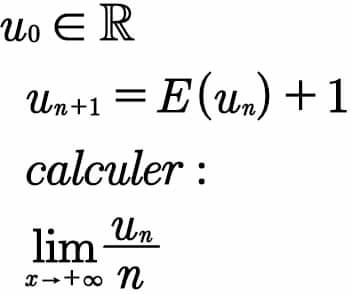
|

|
| calculate ∫_0 ^∞ xe^(−x^2 ) arctan(x−(1/x))dx |
| calculate ∫_1 ^(3 ) ((x−2)/(√(x^2 +x+1)))dx |
| calculate ∫_0 ^∞ ((lnx)/((x+1)^3 ))dx |
| caoculate ∫_0 ^∞ ((arctan(x^2 −1))/(2x^2 +1))dx |
| calculate ∫_0 ^∞ ((ln(2+x^2 ))/(x^2 −x+1))dx |
Pg 1325 Pg 1326 Pg 1327 Pg 1328 Pg 1329 Pg 1330 Pg 1331 Pg 1332 Pg 1333 Pg 1334 |