
Question and Answers Forum
AllQuestion and Answers: Page 1384

Pg 1379 Pg 1380 Pg 1381 Pg 1382 Pg 1383 Pg 1384 Pg 1385 Pg 1386 Pg 1387 Pg 1388
|
Question and Answers Forum |
AllQuestion and Answers: Page 1384 |
| let a>b>0 calculate ∫_0 ^(2π) (dx/((a+bsinx)^2 )) |
| prove that ∀z ∈C we have sinz =z Π_(n=1) ^∞ (1−(z^2 /(n^2 π^2 ))) |
| let z from C−Z prove that (π/(sin(πz))) =(1/z) +Σ_(n=1) ^∞ (((−1)^n 2z)/(z^2 −n^2 )) and ((πcos(πz))/(sin(πz))) =(1/z) +Σ_(n=1) ^∞ ((2z)/(z^2 −n^2 )) |
| calculate A(x) =Σ_(n=1) ^∞ (((−1)^n cos(nx))/n) and B(x) =Σ_(n=1) ^∞ (((−1)^n sin(nx))/n) |
| let f(x,z) =((z e^(xz) )/(e^z −1)) (x and z from C) 1) prove that f(x,z) =Σ_(n=0) ^∞ B_n (x)(z^n /(n!)) with B_n (x) is a unitaire polynome with degre n determine B_n (x) interms of B_n (number of bernoulli) 2)prove that B _n^′ (x)=nB_(n−1) (x) B_n (x+1)−B_n (x) =nx^(n−1) prove that f(x,z)=f(1−x,−z) and B_n (1−x) =(−1)^n B_n (x) |
| if (z/(e^z −1)) =Σ_(n=0) ^∞ B_n (z^n /(n!)) 1) calculate B_0 ,B_1 ,B_2 ,B_3 ,B_4 2)prove that z→(1/(e^z −1))+(1/2) is a odd function conclude that B_(2n+1) =0 for n≥1 |
| if z =x+iy find lnz interms of x and y |
| let z ∈C and ∣z∣<1 prove that (z/(1−z^2 )) +(z^2 /(1−z^4 )) +.....+(z^2^n /(1−z^2^(n+1) ))+...=(z/(1−z)) (z/(1+z)) +((2z^2 )/(1+z^2 )) +....+((2^n z^2^n )/(1+z^2^n )) +....=(z/(1−z)) |
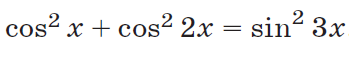
|

|
| ∫x^(n ) lnx/n^x dx |
| Show that 1n^3 + 2n + 3n^2 is divisible by 2 and 3 for all positive integers n. |
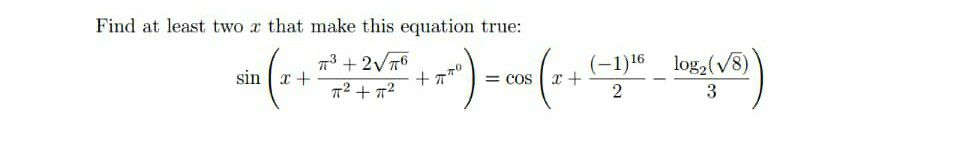
|
| please check my comment to qu. 67471 I′ve been confusing myself... |
| I have tried to solve Q#67299 Please see and give critical remarks |
| Evaluate:∫(√(x(√(x+1)))) dx |
| Find f(x)=∫_0 ^∞ (( tlnt)/((1+t^2 )^x )) dt |
| let consider for all n≥1 the real (t)_n =t(t+1).....(t+n−1) Find L_n = ∫_0 ^∞ (((t)_1 )/((t)_(n+1) )) dt |
| let consider a function g defined by g(a)=∫_0 ^1 (dx/(√((1−x)(1+ax)))) Give the defined Domain of g and simplify g. |
| prove Cos(((2π)/7))+Cos(((4π)/7))+Cos(((8π)/7))=−(1/2) |
| Find Find K=∫_0 ^(π/2) (√(tanθ)) dθ |
| Calculate when a,b are positive reals f(a,b)= ∫_0 ^1 ((t^a −t^b )/(lnt)) dt |
| find the value of Σ_(p=0) ^∞ (((−1)^p )/((2p+1)^2 )) |

|
| p is a prime number such that (1+p)^p ≡2[7] find all k such that p≡k[42] |
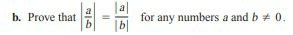
|
Pg 1379 Pg 1380 Pg 1381 Pg 1382 Pg 1383 Pg 1384 Pg 1385 Pg 1386 Pg 1387 Pg 1388 |