
Question and Answers Forum
AllQuestion and Answers: Page 1390



Pg 1385 Pg 1386 Pg 1387 Pg 1388 Pg 1389 Pg 1390 Pg 1391 Pg 1392 Pg 1393 Pg 1394
|
Question and Answers Forum |
AllQuestion and Answers: Page 1390 |
| solve the (de) (2x+1)y^′ +(x^2 −1)y =x^3 e^(−x) |
| find the value of ∫_0 ^∞ (x^2 /(ch(x)))dx |
| find the value of ∫_0 ^∞ (x/(ch(x)))dx |
| (1/1)+(1/2)−(2/3)+(1/4)+(1/5)−(2/6)+(1/7)+(1/8)−(2/9)+(1/(10))+(1/(11))−(2/(12))+∙∙∙= |
| simplify ((x+4)/(x−4))−((5x+20)/(x^2 −16)) |
| without using mathematical tables evaluate ((sin 60.tan 30.cos 60+sin 30.cos 45.sin 45)/(sin 90.cos 45.sin 45−sin 60.cos 30.sin 30)) |
| In a school there are 30 more boys than girls. One-quarter of the boys and two-thirds of the girls are boarders. If there are 255 boarders, find the number of students in the school. |
| Simba had 57 denomination notes which he deposited in his account. He had six times as many two-hundred shilling notes as one-thousand shilling notes and twice as many one-hundred shilling notes as two- hundred shilling notes. The rest were fifty shilling notes. If he deposited a total of sh 7750, find the number of fifty shilling notes he had. |
| By writing your answer in the form a^y simplify (3^(5x) ×5^(2x) ×3^(−x) ÷5^(−2x) )^(1/4) |
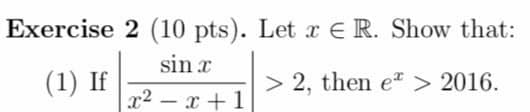
|
| solve the equations, x+y=17 xy−5x=32 |
| solve the simultaneous equations: 3x-y=9 x^2 -xy=4 |
| A rostum is made by cutting off the upper part of a cone along a plane parallel to the base at (2/3) up the height. What fraction of the volume of the cone does the rostum represent? |
| A point T divides a line AB internally in the ratio 5:2. Given that A is (-4,10) and B is (10,3), find the coordinates of T. |
| Each month a store owner can spend at most $100,000 on PC′s and laptops. A PC costs the store owner $1000 and a laptop costs him $1500. Each PC is sold for a profit of $400 while a laptop is sold for a profit of $700. The store owner estimates that at least 15 PC′s but no more than 80 are sold each month. He also estimates that the number of laptops sold is at most half the PC′s. How many PC′s and how many laptops should be sold in order to maximize the profit? |
| ∫_( 0) ^( 1) (√(1−x+x^2 −x^3 )) dx=? |
| find∫(√(dx )) |

|
| y=x^2 −3x y=2x find area |
| ∫_1 ^∞ (1/(x(√(x^2 +1))))=? |
| let U_n =Σ_(k=0) ^n (1/(3k+1)) and H_n =Σ_(k=1) ^n (1/k) calculate U_n interms of H_n |

|
| if f(x)=((ln (x+(√(1+x^2 ))))/(√(1+x^2 ))) f^(−1) (x)=? |

|
| calculate lim_(x→0) ((arctan(1+x^3 )−(π/4))/(xsin(x^2 ))) |
| calculate ∫_0 ^∞ ((cos(arctanx))/(4+x^2 ))dx |
Pg 1385 Pg 1386 Pg 1387 Pg 1388 Pg 1389 Pg 1390 Pg 1391 Pg 1392 Pg 1393 Pg 1394 |