
Question and Answers Forum
AllQuestion and Answers: Page 1423




Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427
|
Question and Answers Forum |
AllQuestion and Answers: Page 1423 |
| Find all solutions of (x, y, a, b) for these equations : x + y^2 = p^a x^2 + y = p^b which x, y, a, b are integers and p prime number . |

|
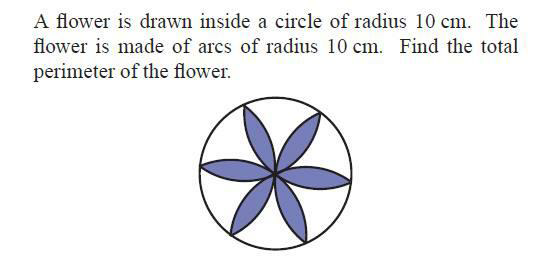
|
| P(α,β) Q(γ,δ) are two points lie on curve tan^2 (x+y)+cos^2 (x+y)+y^2 +2y=0 on XY plane.If d=PQ then cos d= ans:±2nπ,n∈N |
| 32x^3 −48x^2 −22x−3=0 |

|
| The surnames of 40 students in a class were arranged in alphabetical order. 16 of the surnames begin with O while 9 of the surnames begin with A. 14 of the letters of the alphabet do not appear as the first letter of any surname. (i) What is the probability that the surname of a child picked at random from the class begins with either A or O (ii) If more than one surname begins with a letter besides A and O. How many surnames begins with that letter ? |

|
| prove that Σ_(k = 1) ^∞ (1/(k(2k + 1))) = 2 − 2ln(2) |

|

|
| prove that ∫sin^n (x) dx , p∈n , p≥2 =− (1/n)cos(x) sin^(n−1) (x) + (p−1)∫sin^(n−2) (x) dx |
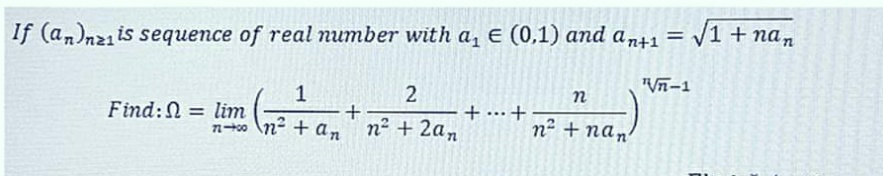
|

|
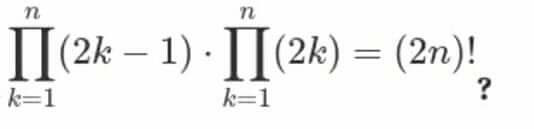
|
| developp at laurent series 1) f(z) =(1/(z−2)) 2)g(z) =(3/(z^2 −3z +2)) 3)h(z) =(1/(z^2 +4)) |
| Calculate ∫_0 ^(1/2) x(√(x^2 +1)) dx+∫_(1/2) ^1 x^2 (√(x^3 +1)) dx+∫_1 ^2 x^3 (√(x^4 +1)) dx+∫_2 ^3 x^4 (√(x^5 +1 ))dx+...+∫_(78) ^(79) x^(80) (√(x^(81) +1)) dx+∫_(79) ^(80) x^(81) (√(x^(82) +1)) dx usingΣ_(n=2) ^(80) ∫_(n−1) ^n x^(n+1) (√(x^(n+2) +1))dx |
| The minimum value of 2x^2 −3x+2 is ___. |
| a) if y= x^m (1−x)^n , where n∈ Z^+ , the set of positive integers, show that when (dy/dx)=0, x=(m/(m+n)) b)if y = 2(x−5)(√(x+4)) ,show that (dy/dx) = ((3(x+1))/((√(x+4)) )) c) solve the equation sinx−sin5x+cos3x = 0 for 0°≤x≤180° |
| find the set of values of x for which y is real if y=(((x−2)(x−1))/(x+2)) , x≠−2, x∈R |
| prove that there exist unique intergers p and s sucb that a = bp + s with −((∣b∣)/2)< s ≤((∣b∣)/2) hence find p and s given that a=49 and b=26 |

|
| consider the general definite intergral I_n =∫_0 ^(π/2) sin^n xdx a) prove that for n≥2, nI_n =(n−1)I_(n−2) . b) Find the values of i)∫_0 ^(π/2) sin^5 dx ii) ∫_0 ^(π/2) sin^6 dx |
| Given that ∣z−6∣=2∣z+6−9i∣, a) Use algebra to show that the locus of z is a circle, stating its center and its radius. b) sketch the locus z on an argand diagram. |
| let f(x)=∫_0 ^∞ (t^(a−1) /(x+t)) dt with x>0 and 0<a<1 1)calculate f(x) 2)calculate g(x)=∫_0 ^∞ (t^(a−1) /((x+t)^2 ))dt 3)find the value of∫_0 ^∞ (t^(a−1) /((1+t)^2 ))dt |
| calculate ∫_(−1) ^1 ((√(1+x^2 )) −(√(1−x^2 )))dx |
Pg 1418 Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 |