
Question and Answers Forum
AllQuestion and Answers: Page 1424


Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428
|
Question and Answers Forum |
AllQuestion and Answers: Page 1424 |

|
| If A=sin^(28) θ+cos^(36) θ then Ans: 0<A≤1 |
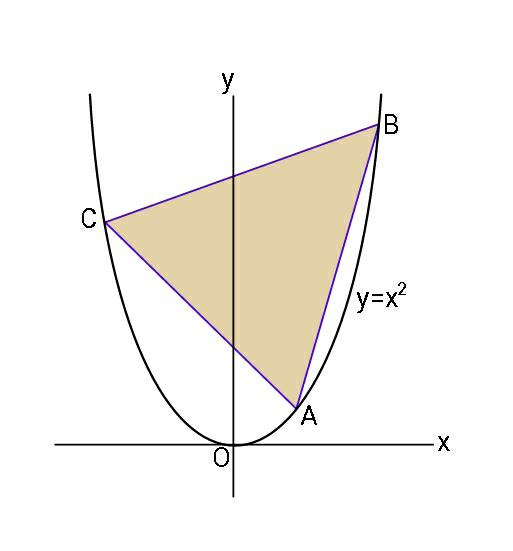
| factorise cosθ−cos3θ−cos5θ +cos7θ |
| question lim_(x→0) ((sin(x+A)−sin(A−x))/(2x)) |
| ((3/4))^x ((2/3))^y =((32)/(27)) find the value of x and yy y. |
| Do you remember that π≈3.1415926535897932⋱ 38462643383279502884⋱ 197... |
| How to calculate ⌈(n) using gamma function ∀n∈R |

|
| ∫_1 ^x x^2 −3x(√x)dx =((−716)/(15)) then calculate ∫_x ^(x+1) (1/(x+3))dx |

|
| It is given that S_n =Σ_(r=1) ^n (3r^(2 ) −3r−1). Use the the formulae of Σ_(r=1) ^n r^(2 ) and Σ_(r=1) ^n r to show that S_n =n^3 . sir Forkum Michael |
| (1) A plane contains the lines ((x+1)/2)=((4−y)/2)=((z−2)/3) and r= (2i+2j + 12k)+t(−i+2j +4k). find (a) the angle between these lines. (b) A cartesian equation of the plane. (2) Given the lines l_1 :((x−10)/3)=((y−1)/1)=((z−9)/4) l_2 :r=(−9j+13k)+μ(i+2j−3k) where μ is a parameter; l_3 :((x+10)/4)=((y+5)/3)=((z+4)/1). a) show that the point (4,−1,1) is common to l_1 and l_2 . Find b) the point of intersection of l_2 and l_3 . c) A vector parametric equation of the plane containing the lines l_2 and l_3 . sir Forkum Michael |
| show that (a) cos[2cos^(−1) (x) +sin^(−1) (x)]= −(√(1−x^2 )) (b) ((sinα + sinβ)/(cosα−cosβ))=cot(((β−α)/2)) (c) 2cos((π/3)+p)≊ 1−(√3) if p is small enough to neglect p^2 . (d) if θ =(1/2)sin^(−1) ((3/4)), show that sinθ−cosθ = ±(1/2) (e)write tan3A in terms of tanA (f) Factorise cosθ − cos3θ−cos5θ+cos7θ (g)i) verify that f(x)=((sin2θ+sin10θ)/(cos2θ+cos10θ))=((2tan3θ)/(1−tan^2 3θ)) ii) hence find in radians the general solution of f(x)=1 sir Forkum Michael |
| The probability that a vaccinated person(V) contracts a disease is (1/(20)). For a person vaccinated(V ′) , the probability of contracting a disease is (5/6). In a certain town 90%of thepopulation has been vaccinated against a disease. A person is selected at random from the town,find the probability that: (a) he has the disease, (b) he is vaccinated or he has the disease. sir Forkum Michael |
| A colony of bacteria if left undisturbed will grow at a rate proportional to the number of bacteria, P present at time,t. However,a toxic substance is being added slowly such that at time t, the bacteria also die at the rate μPt where μ is a positive constant. (a) Show that at time t the rate of growth of the bacteria in the colony is governed by the differential equation (dP/dt)= (k−μt)p where k is apositive constant. when t=0, (dP/dt)=2P and when t=1, (dP/dt)=((19)/(10))P (b) show that (dP/dt)= (1/(10))(20−t)P. Sir Forkum Michael. |
| Prove that ((sin^2 (36°))/(cos^2 (72°)))+sin^2 (72°)cos(36°)=((45+11(√5))/(16)) |
| lim_(x→0) ((2^(sec(x)) − 2^(cos(x)) )/x^2 ) |
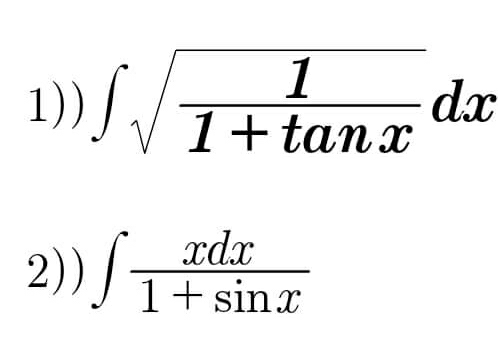
|
| find ∫ (√((x^2 −4x+1)/(x+2)))dx |
| 1) find ∫ ((x+1)/(x^3 −3x −2))dx 2) calculate ∫_4 ^(+∞) ((x+1)/(x^3 −3x +2))dx |
| find a basics of solution of the ode (x^2 −x)y′′ −xy′+y=0 |
| let f(t) =∫_0 ^∞ ((ln(1+tx))/(1+x^2 ))dx with ∣t∣<1 1) determine a explicit form of f(t) 2) find the value of ∫_0 ^∞ ((ln(1+x))/(1+x^2 ))dx |
| solve the equation with using (FPI_Fixed Point Iteration) x−tan(x)=0 , in[4,5] |
| f function integrable on [a,b] is max ∫_a ^b f(x)dx =∫_a ^b maxf(x)dx? if not give a opposite example . |
| solve this equation in all part of complex number: (√((x^9 −3x^2 +1)(x−6)+4))=(x^9 −3x^2 +1)(x−6)−16 |
| solve for both x and n in equation: x^n =216 in all part of integer A {_(n=3) ^(x=6) B{_(n=4) ^(x=5) C{_(n=5) ^(x=4) D {_(n=6) ^(x=3) |
Pg 1419 Pg 1420 Pg 1421 Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428 |