
Question and Answers Forum
AllQuestion and Answers: Page 1427








Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428 Pg 1429 Pg 1430 Pg 1431
|
Question and Answers Forum |
AllQuestion and Answers: Page 1427 |
| y(dy/dx) − (y/(dy/dx)) = 2a a is a real number |
| let f(λ) =∫_0 ^(+∞) (x^4 /(x^6 +λ^6 )) dx with λ>0 1) calculate f(λ) 2) calculate also g(λ) =∫_0 ^∞ (x^4 /((x^6 +λ^6 )^2 ))dx 3) find the values of ∫_0 ^∞ (x^4 /(x^6 +1)) dx , ∫_0 ^∞ (x^4 /(x^6 +8))dx and ∫_0 ^∞ (x^4 /((x^6 +8)^2 ))dx. |
| find ∫ ((x^4 /(1+x^6 )))^2 dx 2) calculate ∫_0 ^1 (x^8 /((1+x^6 )^2 ))dx 3) calculate ∫_0 ^(+∞) (x^8 /((1+x^6 )^2 ))dx . |

|
| Let p(x) = ax^2 + bx + c be such that p(x) takes real values for real values of x and non−real values for non−real values of x . Prove that a = 0 and find all possible values of c. |

|
|
| ∫((cos(x))/x) dx ∫(√(sin(x) )) dx ∫(√(1−k^2 sin^2 (x))) dx k:constant |
| let U_n =∫_0 ^(+∞) ((cos(ch(nx)))/((3+x^2 )^2 ))dx 1) calculate U_n interms of n 2) find lim_(n→+∞) n U_n and lim_(n→+∞) n^2 U_n 3)study the serie Σ U_n |

|

|
| developp at fourier serie f(x) =cos(tx) ,2π periodic even . |

|
| find the value of ∫_0 ^∞ e^(−(t^2 +(1/t^2 ))) dt study first the convergence . |
| let U_n =∫_0 ^(+∞) ((arctan(nt))/(1+n^2 t^2 ))dt with n natural≥1 1) calculate U_n 2) calculate lim_(n→+∞) n^2 U_n 3) study the convergence of Σ U_n |
| 1) find ∫ ((2x^2 −1)/((x+1)(x−3)(x^2 −x+2)))dx 2)calculate ∫_5 ^(+∞) ((2x^2 −1)/((x+1)(x−3)(x^2 −x+2)))dx |
| let f(x) = arctan(nx) with n integr natural 1) calculate f^((n)) (x) and f^((n)) (0) 2) developp f at integr serie . |
| f(t) =∫_0 ^(+∞) (e^(−xt) /((x+t)^2 ))dx with t≥0 1) study the set of definition for f(t) 2)study the continuity of f 3)study the derivability of f 4) developp f at integr serie |
| find the value of ∫_(−∞) ^(+∞) ((x+1)/((x^4 +x^2 +1)^3 ))dx |
| calculate ∫_0 ^(+∞) ((3x^2 −2)/((x^2 +1)( x^2 −2i)^2 )) dx |

|

|

|
| Calculate tg(20°)+4sin(20°)+1 |

|
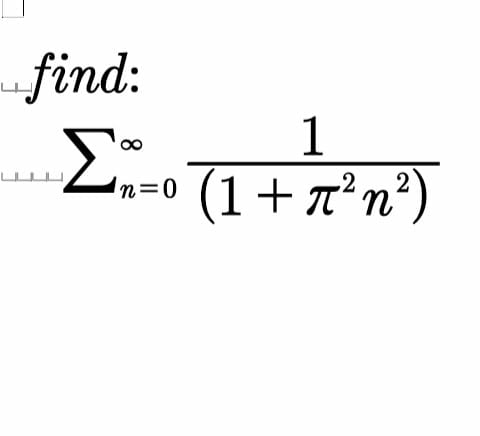
|
Pg 1422 Pg 1423 Pg 1424 Pg 1425 Pg 1426 Pg 1427 Pg 1428 Pg 1429 Pg 1430 Pg 1431 |