
Question and Answers Forum
AllQuestion and Answers: Page 1441





Pg 1436 Pg 1437 Pg 1438 Pg 1439 Pg 1440 Pg 1441 Pg 1442 Pg 1443 Pg 1444 Pg 1445
|
Question and Answers Forum |
AllQuestion and Answers: Page 1441 |

|

|
| if f(z)=Σ_(k=1) ^n a_k z^k ,a_k ,z∈C.Prove a_k =(1/(2πi))∫_(∣z∣=r ) ((f(z))/z^(k+1) )dz |

|
| find ∫ (dx/(sin(2x)+tan(x)))dx |
| solve the (de) (√(2x+1))y^′ −x^3 y = xln(x) |
| use newton method to solve the equation x^4 −3x−1 =0 |
| find ∫ ((x^2 −(√(x−1)))/(2(√(x^2 +3)))) dx |
| find ∫ (dx/(cos(2x)+tan(x))) |
| 3xy^2 +x^3 =9 −−−−−(1) 3x^2 y+y^3 =18−−−−(2) Find x and y |

|
| ∫_(−1) ^1 (((sin(x))/(sinh^(−1) (x))))(((sin^(−1) (x))/(sinh(x)))) dx =? |
| Find the maximum volume tetrahedron inside an ellipsoid, parameters a,b,c . |
| calculate A =∫_0 ^∞ cos(x^n )dx and B =∫_0 ^∞ sin(x^n )dx with n≥2 (n integr natural) |
| ∫(dx/(2+sin(x))) |
| 8+(4+3×2) |
| 6^(−3) |
| (7^(10) /7^7 ) |
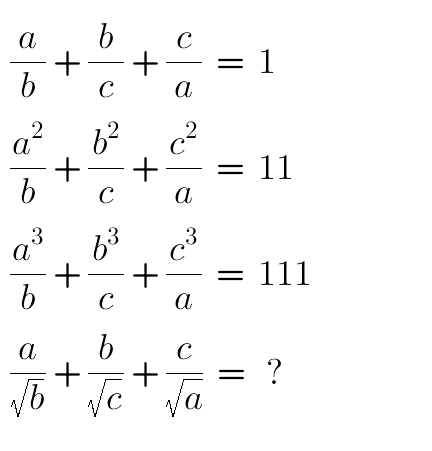
|
| if(3/2)≤x≤5, prove:2(√(x+1))+(√(2x−3))+(√(15−3x))<2(√(19)) |
| f(x)=(√(x^4 −3x^2 +4))+(√(x^4 −3x^2 −8x+20)) find the minimum value of f(x) |

|
| Σ_(n≥0) n^2 x^n |
| calculate ∫_(−(π/4)) ^(π/4) ((cosx)/(e^(1/x) +1)) dx |
| 1) calculate ∫∫_R^+^2 ((dxdy)/((1+x^2 )(1+y^2 ))) 2) find the value of ∫_0 ^∞ ((ln(x))/(x^2 −1)) dx . |
| let U_n = ∫_0 ^∞ (dt/((1+t^3 )^n )) dt (n≥1) 1) calculate (U_(n+1) /U_n ) 2) study the serie Σln((U_(n+1) /U_n )) and prove that lim_(n→+∞) U_n =0 |
Pg 1436 Pg 1437 Pg 1438 Pg 1439 Pg 1440 Pg 1441 Pg 1442 Pg 1443 Pg 1444 Pg 1445 |