
Question and Answers Forum
AllQuestion and Answers: Page 1444





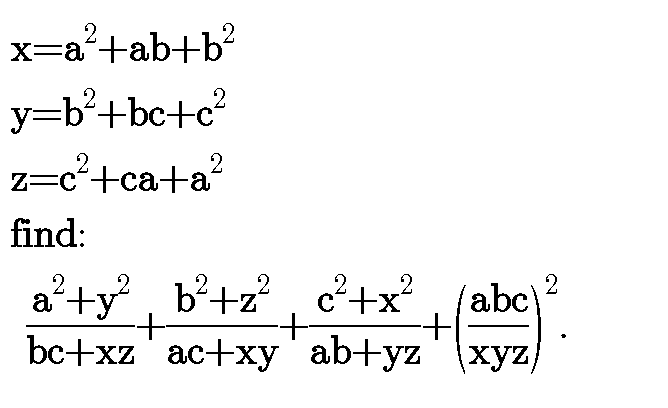



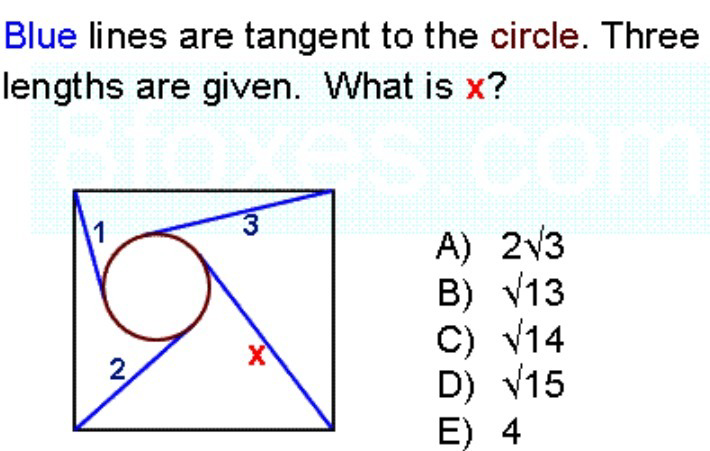
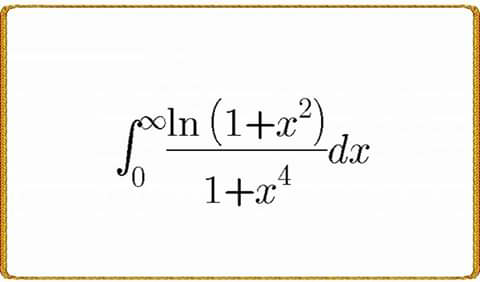
Pg 1439 Pg 1440 Pg 1441 Pg 1442 Pg 1443 Pg 1444 Pg 1445 Pg 1446 Pg 1447 Pg 1448
|
Question and Answers Forum |
AllQuestion and Answers: Page 1444 |
| find ∫_0 ^1 ((sinx)/(1+x^2 ))dx |

|
| solve for x: x^4 −x=12 |

|
| how to calculate lim_(n→+∞) 0.05^(0.05^(0.05^.^.^(.0.05) ) ) }n in a simple and fast way? |

|
| A container is 50% full of water at triple point phase . It′s Isolated and subjected to space system defining no gravity acting on the particles , Which state of matter is now more dominant , solid , liquid , or gas ? Calculate the intermolecular distances between simultaneous two distinct states of water. |
| (998^(999) × 999^(998) × 2019^(2019) ) mod (1000) = ? |
| (x+y)(x^2 +y^2 )(x^3 + y^3 ) = 2 (x^4 +y^4 )(x^6 +y^6 )(x^8 + y^8 ) = 4 (x^3 + y^3 )(x^5 + y^5 )(x^7 + y^7 ) = 6 (x^4 + y^4 )(x^5 + y^5 )(x^9 + y^9 )(x^(10) + y^(10) ) = ? |
| If p , x_1 ,x_2 ,...x_i and q,y_1 ,y_2 ,...y_i form two infinite arithmetic sequences with common difference a and b respectively , then find the locus of the point ( α , β ) where α = (1/n) Σ_(i=1) ^n x_i and β= (1/n) Σ_(i=1) ^n y_(i .) |

|
| Suppose α ,β,γ,δ are real numbers such that α+β+γ+δ = α^7 +β^7 +γ^7 +δ^7 =0 Prove that α(α+β)(α+γ)(α+δ)=0 |

|
| Let p(x) be a quadratic polynomial such that for distinct α and β , p(α) = α and p(β) =β prove that α and β are roots of p[p(x)]−x=0 Find the remaining roots . |
| Let a,b,c,d,e ≥ −1 and a+b+c+d+e=5 Find the maximum and minimum value of S =(a+b)(b+c)(c+d)(d+e)(e+a) |
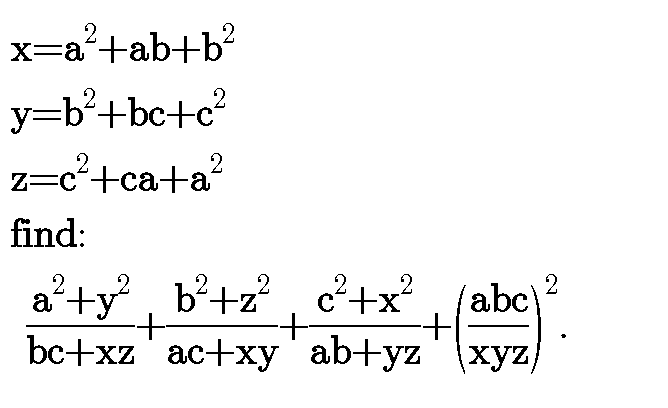
|
| for polynomial p(x),the value of p(3) is −2.which of the following must be true about p(x)? (a)x−5 is the factor of p(x) (b)x−2is the factor of p(x) (c)x+2 is the factor of p(x) (d)the reminder when p(x) is divide d by x−3 is −2 |
| Calculate, using cartesian coodinates, the following integrals: 1) ∫∫_D dxdy being D={ (x,y)∈R^2 /0≤x≤(1/2),y+x≤1,y≥0} 2) ∫∫_D x^3 ydxdy being D={(x,y)∈R^2 /0≤x≤(1/2),y+x≤1,y≥0} 3) ∫∫_D (x/y)dxdy being D={(x,y)∈R^2 /xy≤16,x≥y,x−6≤y,x≥0,y≥1} Help please! |

|
| ∫ ((x^(2 ) − 4)/((x^2 + 4)^2 )) dx |

|

|
| let U_n =∫_1 ^(+∞) (([nx]−[(n−1)x])/x^3 ) dx with n≥1 1) find U_n interms of n 2) find lim_(n→+∞) U_n 3) study the serie Σ_(n=1) ^∞ U_n |
| let f_n (a) =∫_0 ^a x^n (√(a^2 −x^2 ))dx with a>0 1) determine a explicit form of f(a) 2) let g_n (a) =f^′ (a) give g_n (a) at form of integral and give its value 3) find the value of ∫_0 ^2 x^3 (√(4−x^2 ))dx and ∫_0 ^(√3) x^4 (√(3−x^2 ))dx |

|
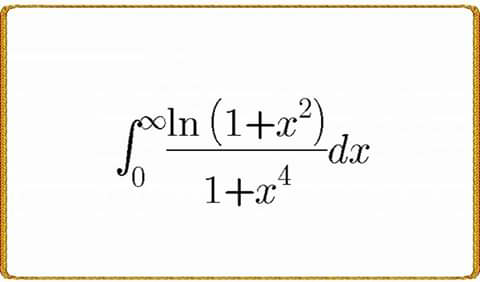
|
Pg 1439 Pg 1440 Pg 1441 Pg 1442 Pg 1443 Pg 1444 Pg 1445 Pg 1446 Pg 1447 Pg 1448 |