
Question and Answers Forum
AllQuestion and Answers: Page 1472


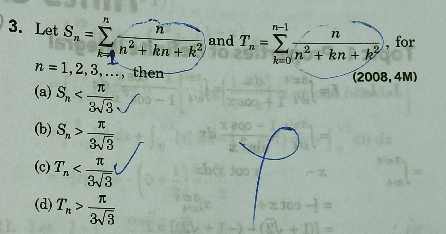



Pg 1467 Pg 1468 Pg 1469 Pg 1470 Pg 1471 Pg 1472 Pg 1473 Pg 1474 Pg 1475 Pg 1476
|
Question and Answers Forum |
AllQuestion and Answers: Page 1472 |
| let f(x)=∫_(2x) ^(4x) (dt/(t^2 −2t +3)) 1)find f(x) 2) calculate lim_(x→0) f(x) and lim_(x→+∞) f(x) |
| solve (x−1)y^′ +(1+(√x))y =x e^(−2x) |
| solve y′ =2y^2 +y and y(o)=1 |
| prove that ln(1+x)>((arctanx)/(1+x)) ∀x>0 |
| let u_n =1 +(1/(√2)) +(1/(√3)) +...+(1/(√n)) prove that (u_n ) is divdrgente. |
| let f(x)=arctan((√x)+(√(x+1))) find f^(−1) (x) . |
| find lim_(x→1) ((sin(x^5 +x−2))/(x−1)) |
| let S_n =Σ_(k=1) ^(2n+1) (1/(√(n^2 +k))) calculste lim_(n→+∞) S_n |
| let the sequence (a_n ) wich verify a_1 =2 and a_(n+1) =a_n +(√(1+(a_n /n))) prove that ((a_n /n))_(n≥1) is convergente. |
| let U_0 =cos((π/3)) and U_(n+1) =(√((1+U_n )/2)) find U_n interms of n . |
| let f(x)=(x/(√(1+x^2 ))) +cos(πx) 1) prove that f(x)=0 have a solurion α inside ]0,1[ 2) use newton method to find a approximate value of α . |
| calculate lim_(x→0) ((1−cosx.cos(2x)....cos(nx))/x^2 ) with n integr natural not 0. |
| find lim_(x→0) ((sin(π(√(cosx))))/x^2 ) |

|
| a^2 + d^2 − ad = b^2 + c^2 + bc a^2 + b^2 = c^2 + d^2 ((ab + cd)/(ad + bc)) = ? |
| If aεR and the equation : −3{x}^2 +2{x}+a^2 =0 has no integral solution, then all possible value of a lie in the interval : (a)(−1,0)U(0,1) (b)(1,2) (c) (−2,−1) (d)(−∞,−2)U(2,∞) |
| Given f(x) = f(x + 2016), ∀x ∈ R If ∫_0 ^3 f(x) = 30, then ∫_3 ^5 f(x + 2016) = ... |

|
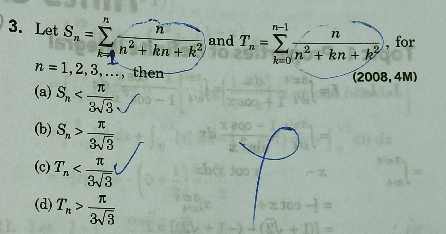
|

|

|
| Can i find the sum of a product to infinity ? e.g 1.2.3.4.5 .... infinity |
| tan 1°+tan 5°+tan 9°+…+tan 177°=... |
| 5^(3x−3) −5^(3x) −5=615 solve for x |

|
| 1−2sin(4x)<cos^2 (4x) solve. |
Pg 1467 Pg 1468 Pg 1469 Pg 1470 Pg 1471 Pg 1472 Pg 1473 Pg 1474 Pg 1475 Pg 1476 |