
Question and Answers Forum
AllQuestion and Answers: Page 1479




Pg 1474 Pg 1475 Pg 1476 Pg 1477 Pg 1478 Pg 1479 Pg 1480 Pg 1481 Pg 1482 Pg 1483
|
Question and Answers Forum |
AllQuestion and Answers: Page 1479 |
| calculate ∫∫_D ((x+y)/(3+(√(x^2 +y^2 ))))dxdy with D={(x,y)∈R^2 /x^2 +y^2 ≤2 and x≥0 ,y≥0} |
| calculate ∫∫_D (x−y)(√(x^2 +y^2 ))dxdy with D ={ (x,y)∈R^2 /x^2 +y^2 ≤2 and x≥0} |
| calculate ∫∫_D xy e^(−x^2 −y^2 ) dxdy with D={(x,y)∈R^2 / 0≤x≤2 and 1≤y≤3} |
| calculate ∫∫_D e^(x−y) dxdy with D={(x,y)∈R^2 /∣x∣<1 and 0≤y≤1} |

|

|
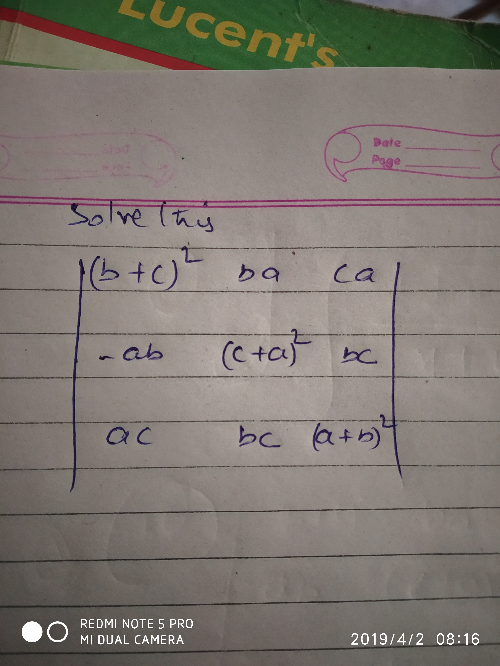
|

|

|
| Tangents are drawn to x^2 +y^2 =16 from the point P(0,h).These tangents meet the x−axis at A and B. If area of ΔPAB is minimum then find value of h ? |
| y is varies directly as the square of x and inversely as z. if x is inceased by 10% and z is decreased by 20%, find the percentage change in y. |

|
| If A>0,B>0, and A+B=(π/3) , then maximum value of tanAtanB is ? |
| lim_(x→0) ((e^x + e^(−x) )/x) |

|
| ((a^8 +a^4 +1)/(a^4 +a^2 +1))=? |

|
| find f(x) =∫_1 ^2 ((ln(1+xt))/t^2 ) dt with x>0 |
| let f(α)=∫_0 ^1 ((arctan(αx))/(1+αx^2 )) dx with α real 1) find f(α) interms of α 2) find the values of ∫_0 ^1 ((arctan(2x))/(1+2x^2 )) dx and ∫_0 ^1 ((arctan(4x))/(1+4x^2 ))dx |
| calculate A_n =∫_0 ^1 x^n (√((1−x)/(1+x)))dx with n integr natural |
| find the value of ∫_0 ^1 ((3t^2 −5t +1)/((t+1)(t+2)(2t+3)))dt |
| 1)calculate f(a) =∫_0 ^a ((2x−1)/((x^2 −x+3)(x^2 +1)))dx 1) calculate f(1)and f(2) |
| Express 5.27 in form of a series and show that is equal to 5 (5/(18)) |
| ∫((×(√(x+1)))/(x+2))dx |
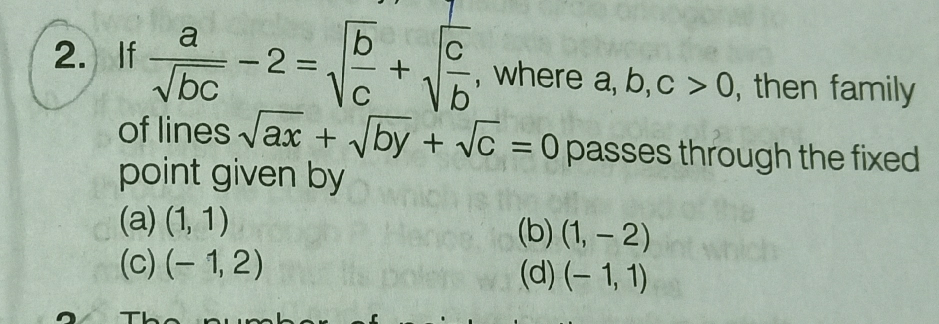
|
| let A_n =∫_n ^n (([(√(x+1))]−[(√x)])/x) dx with n natural integr and n≥1 1) find A_n interms of n 2)find nature of the serie Σ A_n |
Pg 1474 Pg 1475 Pg 1476 Pg 1477 Pg 1478 Pg 1479 Pg 1480 Pg 1481 Pg 1482 Pg 1483 |