
Question and Answers Forum
AllQuestion and Answers: Page 1492


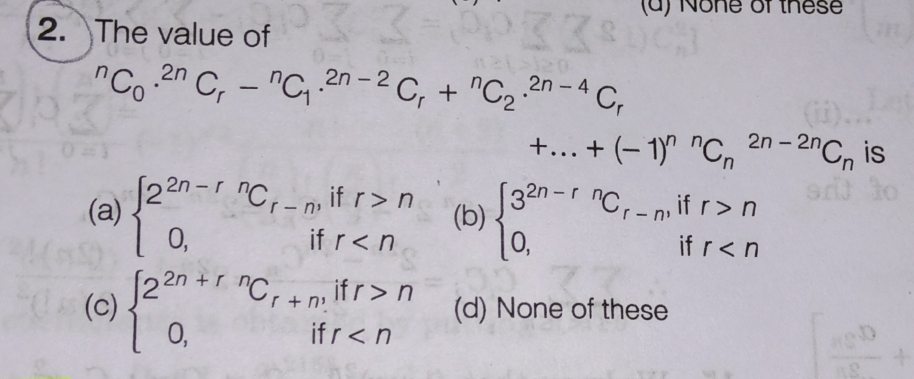
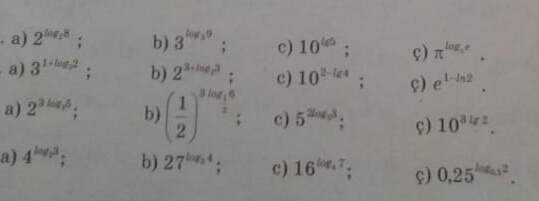
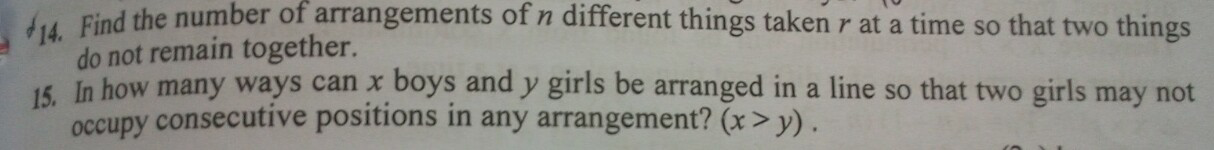
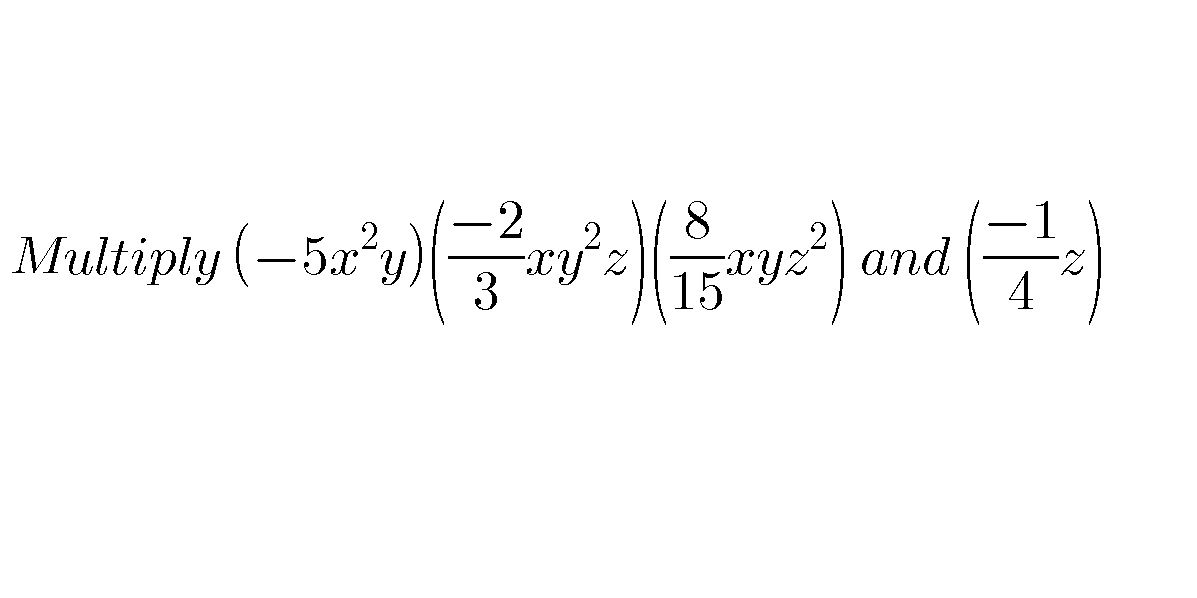




Pg 1487 Pg 1488 Pg 1489 Pg 1490 Pg 1491 Pg 1492 Pg 1493 Pg 1494 Pg 1495 Pg 1496
|
Question and Answers Forum |
AllQuestion and Answers: Page 1492 |
| question 54995 reposted ∫((x^3 +x^2 ))^(1/3) dx=? |

|
| How many numbers, divisible by 5, can be made with the digits 2,3,4 and 5 where no digit is being used more than once in each number? |

|
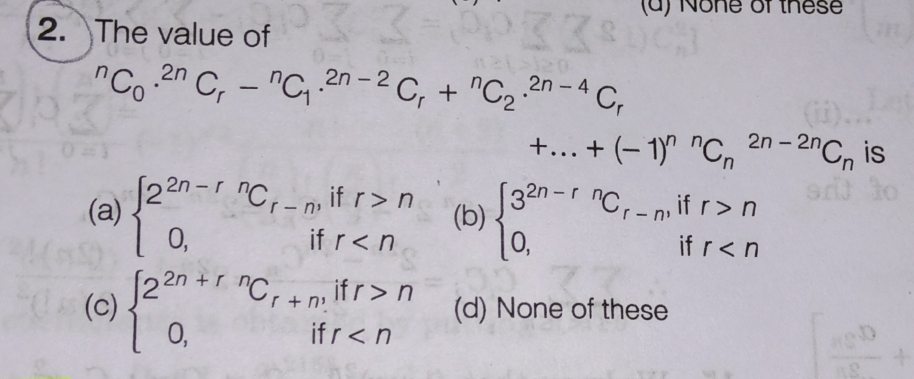
|
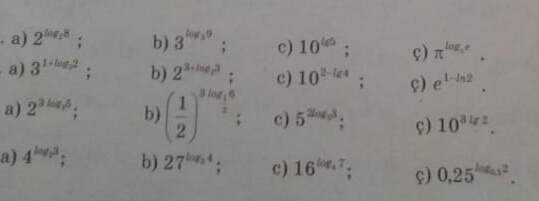
|
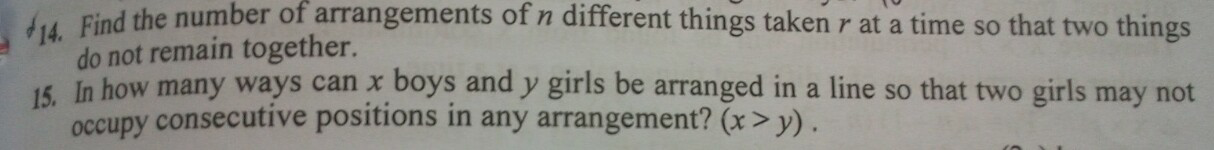
|
| Show that for n ∈ N, Σ_(r=0) ^n P_r ^n = ⌊n! e⌋ where ⌊x⌋ denotes the greatest integer ≤ x and P_r ^n = ((n!)/((n − r)!)) |
| ∫_( 0) ^1 (1/((x^2 +1)^(3/2) )) dx = |
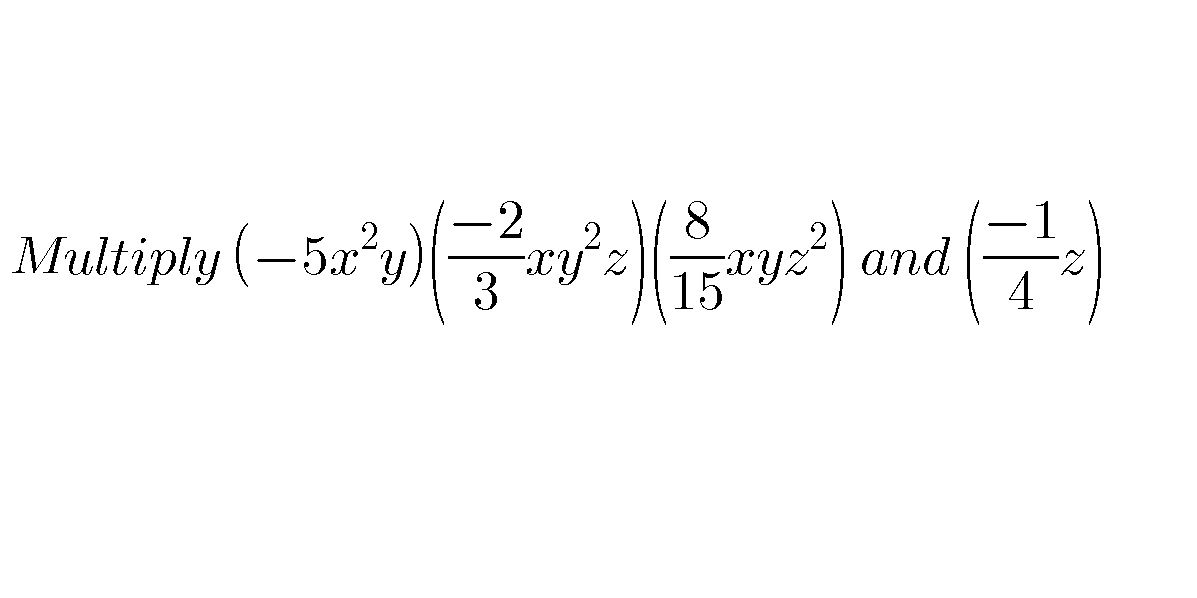
|
| Please any web site or ebook to learn LATEX ? Thank you. |
| (((1/4) + (1/(16)) + (1/(36)) + (1/(64)) + ...)/(1 + (1/9) + (1/(25)) + (1/(49)) + ...)) = x 3x^2 + 2x − 1 = ? |

|
| Known polynom P(z)=a_0 z^n +a_1 z^(n−1) +…+a_(n ) With explain real number. If z_0 =3−4i form root is from polynom, then one other root defonitely appeared is.. |
| Factorised the polynom z^4 +1 be polynom with lower degree, but have real coefficient |
| Known analytic function f(z)=((2(z−2))/(z(z−4))) and written as f(z)=Σ_(n=0) ^(∝) a_n (z−1)^n The value of a_(100) is... |
| Calculate value of ∫_C e^(2/z) dz if C is unit circle |
| Known C circle centered at 0. Find value than ∫_C (dz/(1−z)) |
| Find radius convergence for series 1−z^2 +z^4 −z^6 +... |
| Find the number of root equation z^4 −5z+1=0 in 1 ≤ ∣z∣ ≤ 2 |
| Prove that: P_n (z)=a_0 z^n +a_1 z^(n−1) +...+a_(n−1) z+a_n at least have one value of zero |
| Prove that Ln(z+1)=z−(z^2 /2)+(z^3 /3)−(z^4 /4)+... for ∣z∣< 1 |

|

|

|
| calculate lim_(n→+∞) ∫_0 ^1 (dx/(1+x+x^2 +...+x^n )) |
Pg 1487 Pg 1488 Pg 1489 Pg 1490 Pg 1491 Pg 1492 Pg 1493 Pg 1494 Pg 1495 Pg 1496 |