
Question and Answers Forum
AllQuestion and Answers: Page 1504




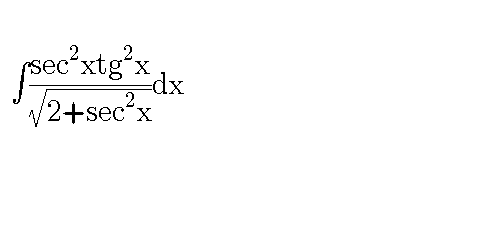

Pg 1499 Pg 1500 Pg 1501 Pg 1502 Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508
|
Question and Answers Forum |
AllQuestion and Answers: Page 1504 |
| ∫ e^(2x) ((1/x) −(1/(2x^2 )))dx ∫e^(2x) (((1+sin 2x)/(1+cos 2x)))dx. Solve above Questions by using the formulae : ∫e^(kx) {f(kx)+f ′(kx)}dx= e^(kx) f(kx)+c. |
| How many words with at least 2 letters can be formed using the letters from TINKUTARA? |

|
| simplify A_n =Σ_(k=0) ^n k^2 C_n ^k cos(kθ) and B_n =Σ_(k=0) ^n k^2 C_n ^k sin(kθ) . |
| f(x)=((2[x])/(3x−[x])) examine its continuity at x=((−1)/2) where [x] is greatest integer function |
| y = cos2t×sen2t y′ = ? |

|

|

|
| show that a. Σ_(r=1) ^(n) r^3 ._n C_r =n^2 (n+3).2^(n−3) b. _n C_0 ._n C_1 +_n C_1 ._n C_2 +...+_n C_(n−1) ._n C_n =(((2n)!)/((n−1)!.(n+1)!)) |
| Such That a. _(n+1) C_r =(((n+1). _n C_r )/((n−r+1))) b. _n C_0 +_n C_2 +_n C_(4...) =_n C_1 +_n C_3 +_n C_(5...) =2^(n−1) |
| A= [(3,7),((−1),(−2)) ] A^(27) +A^(31) +A^(40) =... |
| Given f(x) = ((4x + (√(4x^2 − 1)))/((√(2x + 1)) − (√(2x − 1)))) Find the value of f(13) + f(14) + f(15) + ... + f(112) |
| ((1+sinx+cox)/(1+sinx−cosx))=((1−cosx)/(1+cosx)) |
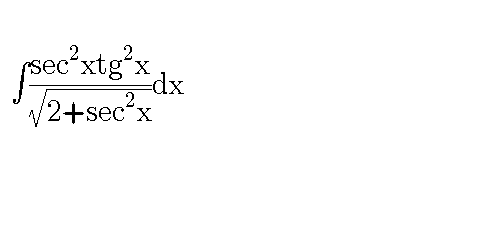
|
| If ((u^5 +v^5 )/((u+v)^5 )) = −(1/5) , find ((u^3 +v^3 )/((u+v)^3 )) = ? |
| a,b,c ,are nonnegative real numbers and: a+b+c=1 . show that: 0≤ ab+bc+ca−2abc ≤(7/(27)) . |
| in a given triangle: tg(C/2)=((a.tgA+b.tgB)/(a+b)) . define the kind of triangle. |
| solve for: x 1) (√(3−x))+(√(x+1))>(1/2) 2) cos^2 x+cos^2 2x+cos^2 3x=1 3)(√(x^2 −p))+2(√(x^2 −1))=x [p∈R] |
| x+y=a z+bx=c bz+xy=d Find yz in terms of a,b,c,d. |
| What is : (d/dx) [ u(x) × v(x) × w(x) ] = ... and more generally, what is : (d/dx) [ Π_(i=1) ^n u_i (x)] = ... Thank you |
| (√(1−x^2 )) + (√(1−y^2 )) = a(x−y) prove that (dy/dx)=(√((1−y^2 )/(1−x^2 ))) |
| show that ∫_0 ^∞ (x/(1+x^6 ))dx=(π/(3(√3))) |

|
| Solve for x: (1/(√(x + (√x) + 1))) + (2/(√(x + (√x) − 2))) = (√(x + 1)) |
| A particle of mass 1.5kg rests on a rough plane inclined at 45° to the horizontal. It is maintained in equilibrium by a horizontal force of p newtons. Given that the coefficient of friction between the particle and the plane is (1/4), calculate the value of p when the particle is on the point of moving i. down the plane ii. up the plane [take g=10ms^(−2) ]. |
Pg 1499 Pg 1500 Pg 1501 Pg 1502 Pg 1503 Pg 1504 Pg 1505 Pg 1506 Pg 1507 Pg 1508 |