
Question and Answers Forum
AllQuestion and Answers: Page 1608

Pg 1603 Pg 1604 Pg 1605 Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612
|
Question and Answers Forum |
AllQuestion and Answers: Page 1608 |
| let f(a) = ∫_(−∞) ^(+∞) cos(ax^2 )dx with a>0 1) calculate f(a) interms of a ) calculate ∫_(−∞) ^(+∞) cos(2x^2 )dx 3) find the value of ∫_(−∞) ^(+∞) cos(x^2 +x+1)dx . |
| let f(x) = ∫_(−∞) ^(+∞) ((cos(xt))/((t−i)^2 )) dt 1) let R =Re(f(x)) and I =Im(f(x)) extract R and I 2) calculate R and I 3) conclude the value of f(x) 4) calculate ∫_(−∞) ^(+∞) ((cos(2t))/((t−i)^2 ))dt 5) let u_n = ∫_(−∞) ^(+∞) ((cos((t/n)))/((t−i)^2 ))dt (n natral integer not o) find lim_(n→+∞) u_n and study the convergence of Σu_n |
| Solve : 2x^2 ydx −2y^4 dx+2x^3 dy+3xy^3 dy=0. |
| a + b + c = 180 a,b,c ∈ N number of triplets possible (a,b,c) for the above equation are ? ( the order of a,b,c doesn′t matter) |
| let f(x) =e^(−∣x∣) , 2π periodic even developp f at fourier serie . |
| Solve: (dt/dx) = (2/(x+t)) . |
| Number of straight lines which satisfy the differential equation (dy/dx) + x((dy/dx))^2 − y =0 is ? |
| Find the equation of tangent and normal to the curve y given by y = x^3 + 3x^2 + 7 . |
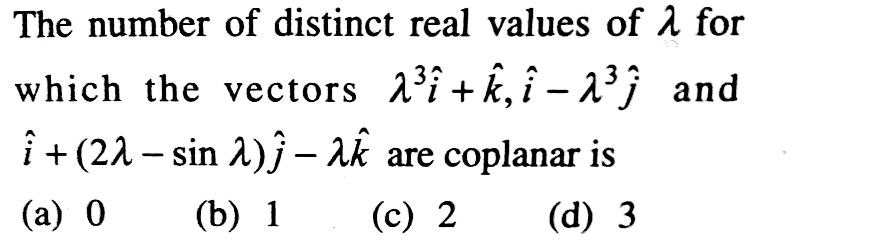
|

|
| Let P be an interior point of a triangle ABC and AP,BP,CP meet the sides BC, CA,AB in D,E,F respectively. Show that ((AP)/(PD))= ((AF)/(FB)) + ((AE)/(EC)) . |
| let p(x)=x^(10) −1 1) find roots of p(x) 2) factorize i nside C[x] p(x{ 3) factorize inside R[x] p(x) . |
| ∫_( 0) ^(2a) ((f(x))/(f(x)+f(2a−x))) dx = |
| let A_p =∫_0 ^∞ ((sin(px))/(e^x −1)) dx with p>0 1)give A_p at form of serie 2) give A_1 at form of serie . |
| let u_n =Σ_(k=1) ^n (((−1)^k )/(√k)) 1) prove that (u_n )is convergente 2) find a equivalent of u_n when n→+∞ |
| calculate f(x) = ∫_0 ^∞ e^(−t^2 ) arctan(xt^2 )dt |
| let x>0 calculate f(x) =∫_0 ^(+∞) e^(−t) ∣sin(xt)∣ dt |
| study the convergence of Σ_(k=0) ^∞ e^(−i((kπ)/x)) and find its sum |
| integrate ∫e^x^2 x^2 dx |
| calculate ∫_0 ^(2π) (dθ/((1+cosθ)^3 )) |
| The median AD of triangle ABC is bisected at E and BE meets AC at F. Find AF:FC . |
| 81(√) |
| sin3x+sin5x=2(cos^2 2x−sin^2 3x) |
| cos^2 3xcos2x−cos^2 x=0 |
| (2tanx−5)tanx+(2cotx−5)cotx−8=0 |
| solve 2sin3x(sinx+(√3)cosx)+1+2cos2x=0 |
Pg 1603 Pg 1604 Pg 1605 Pg 1606 Pg 1607 Pg 1608 Pg 1609 Pg 1610 Pg 1611 Pg 1612 |