
Question and Answers Forum
AllQuestion and Answers: Page 1621






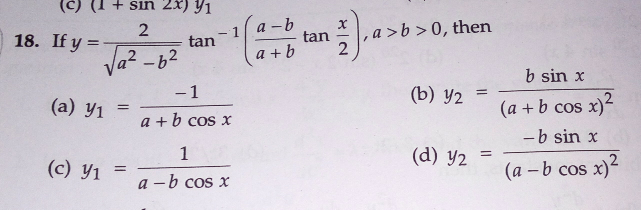
Pg 1616 Pg 1617 Pg 1618 Pg 1619 Pg 1620 Pg 1621 Pg 1622 Pg 1623 Pg 1624 Pg 1625
|
Question and Answers Forum |
AllQuestion and Answers: Page 1621 |
| a piece of wire 40cm long is cut into two parts and each part is then bent into a square.if the sum of these squares is 68cm^2 find the lengths of the two pieces of wire. |

|
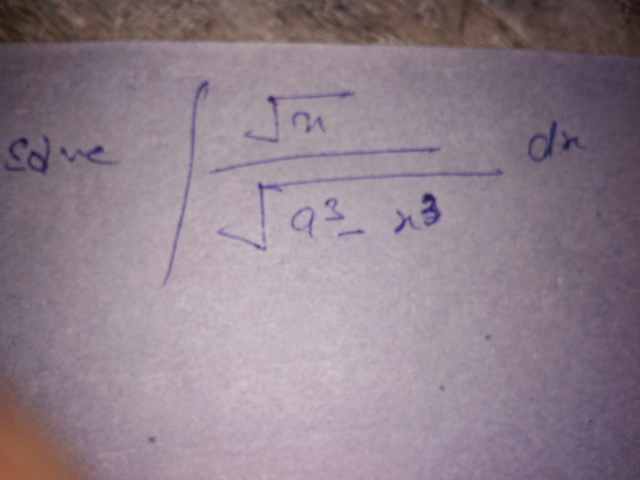
| find ∫ ((√(1+x^2 ))/(√(1−x^3 ))) dx |
| calculate lim_(n→+∞) ((1−e^(−nx^2 ) )/(x^2 sin((π/n)))) |

|

|

|

|

|
| ∫(√(tanx/sinx.cosxdx)) |
| ∫(cosx−cos2x/1−cosx)dx |
| for x≥2 ∣x−2∣= |
| Two point charges,q_1 =0.4μC and q_2 =−0.3μC are placed at 10cm apart.Calculate (a)the potential at point A which is midway between them,and (b)point B which is 6cm from q_1 and 8cm from q_2 |
| calculate lim_(x→0) ((cos(x−sinx)−1)/(x^2 )) |
| A charge q_1 =2.0×10^(−9) C is placed at the point,(x=0,y=4cm) and another charge,q_2 =−3.0×10^(−9) C is located at the point,(x=3cm,y=4cm). If a third charge,q_3 =4.0×10^(−9) C is placed at the origin, a)obtain the x and y component of the total force on q_3 b)Calculate the magnitude and direction of the total force on q_(3.) |
| Two point charges q_1 =1.5×10^(−9) C and q_2 =3.0×10^(−9) C are seperated by a distance of 200cm.Calculate the point at which the total electric field is zero. |

|
| ∫((x^7 −1)/(logx))dx |

|
| find the value lim_(x→0) g(x) must have, if g complies the statement about limit. Suppose lim_(x→ −4) [x lim_(x→0) g(x)] = 2 |
| −5−( )=3 −5−x=3 x=3+5 x=8(give sign of greater number) −5−8=3 |
| Factorise: x^(19) − x^(17) + x^(10) + x^8 + 1 |
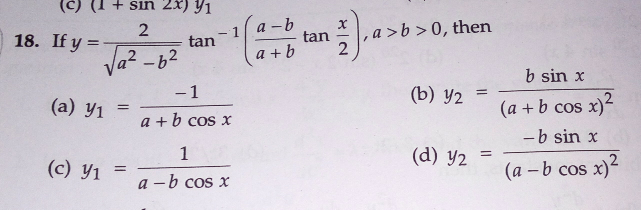
|
| 1)find g(x)=∫_0 ^(π/2) ln(1−x^2 cos^2 θ)dθ with x from R 2) find the value of ∫_0 ^(π/2) ln(1−2 cos^2 θ)dθ and 3) find the value of A(α)=∫_0 ^(π/2) ln(1−cos^2 α cos^2 θ)dθ |
| let f(t) = ∫_0 ^∞ ((arctan(tcosx))/(1+x^2 ))dx 1) find another form of f(t) 2) calculate ∫_0 ^∞ ((arctan(2cosx))/(1+x^2 ))dx . |
| find ∫_0 ^(π/4) ((x−1)/(2+cosx))dx . |
Pg 1616 Pg 1617 Pg 1618 Pg 1619 Pg 1620 Pg 1621 Pg 1622 Pg 1623 Pg 1624 Pg 1625 |