
Question and Answers Forum
AllQuestion and Answers: Page 1625

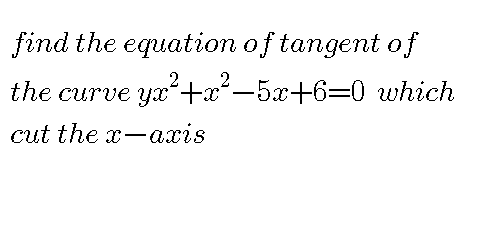




Pg 1620 Pg 1621 Pg 1622 Pg 1623 Pg 1624 Pg 1625 Pg 1626 Pg 1627 Pg 1628 Pg 1629
|
Question and Answers Forum |
AllQuestion and Answers: Page 1625 |
| calculate lim_(x→1) ((1+cos(πx))/(x^2 − sin(((πx)/2)))) |
| find the value of f(x) = ∫_0 ^π ln(x^2 −2x cosθ +1)dθ with x fromR. |
| let S_n = Σ_(k=1) ^n (1/(k(√k))) find a equivalent of S_n (n→+∞) |
| let S_n = Σ_(k=1) ^n (1/(√k)) find a equivalent of S_n when n →+∞ |

|
| Two equal charges q_1 =q_(2 ) =−6μC are on the y−axis at y_1 =3cm and y_2 =−3cm. i)What is the magnitude and direction of the electric field on the x−axis at x= 4cm, ii)if a test charge q_0 =2μC is plqced at x=4cm,find the force the net charge experiences. |
| Two charges Q_0 and 3Q_0 are at l distance apart.These two charges are free to move but do not because is a third charge nearby.What must be the charge for the first two to be in equilibrium? |

|
| write the expression of electrostatic force between two charges Q_(1 ) and Q_2 separated by distance r. for the following condition 1)in air 2)when die electric present between them 3)when die electric partially fill space betweenp them |
| find the minimum and maximum value of the quadratic functions a) 4x^2 + 5x + 1 b) x + (2/x) = 3 c) x^2 − (x/4) + 6 hence draw each draw |
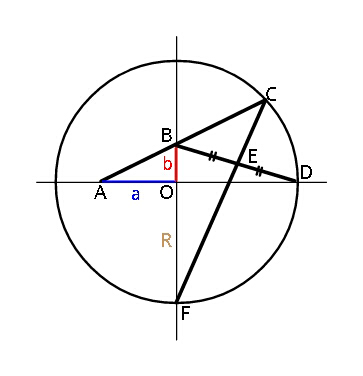
| Given the lines l_1 :−3mx + 3y = 9 and l_(2 ) : y = mx + c find the value of m and c if the point (1,2) lie on both lines. hence the tangent of the curve y = (mx + c)^2 when it moves across the x−axis |
| if cos A= (3/5) and tan B = ((12)/5) where A and B are reflex angles find without using tables,the value of a) sin (A − B) b) tan(A−B) c) cos (A + B). |
| Solve for x in the range 0 ≤ x ≤2π the equations a) cos(x + (π/3)) = 0 b) sin x = cos x. c) sin 2x + 2sin x = 1 + cos x |
| show that a) ((1 + 2sin2θ − cos2θ)/(1+sin2θ + cos 2θ)) = tan θ b) tan^2 A − tan^2 B = ((sin^2 A−sin^2 B)/(cos^2 A cos^2 B)) |
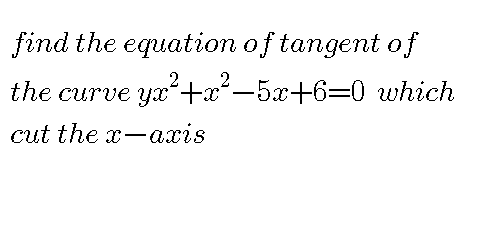
|
| Point charges 88μC,−55μC and 70μC are placed in a straight line. The central one is 0.75m from each of the others.Calculate the net force on each due to the other two. |

|

|
| if (1+x)^n =Σ_(i=0) ^n a_i x^i and (1+x)^(n+1) =Σ_(i=0) ^(n+1) b_i x^i calculate ((∐_(i=0) ^n a_i )/(Π_(i=0) ^(n+1) b_i )) . |
| simplify 1) A_n =(1/(√a)){ (((1+(√a))/2) )^n −(((1−(√a))/2))^n } with n natural integr and a>0 2) f(x)= (1/(√(2x+1))){ (((1+(√(2x+1)))/2))^n −(((1−(√(2x+1)))/2))^n } |
| find radius of S(x)=Σ_(n=1) ^∞ (x^n /n^2 ) and calculate its sum 2) find Σ_(n=1) ^∞ (1/n^2 ) and Σ_(n=1) ^∞ (1/(n^2 2^n )) . |

|

|

|
| sin θ=sin αsin (((θ+α)/2)) Express θ explicitly in terms of α. |
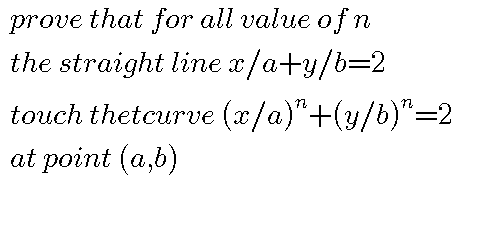
|
Pg 1620 Pg 1621 Pg 1622 Pg 1623 Pg 1624 Pg 1625 Pg 1626 Pg 1627 Pg 1628 Pg 1629 |