
Question and Answers Forum
AllQuestion and Answers: Page 1681
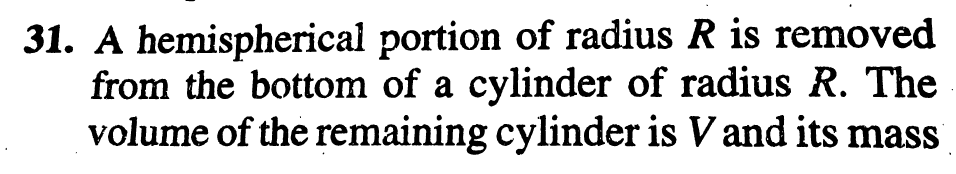
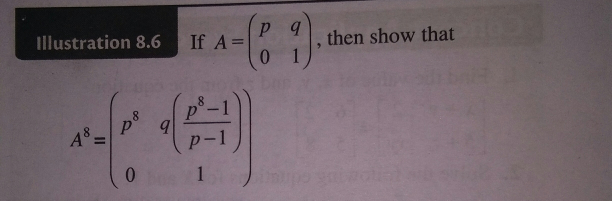
Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682 Pg 1683 Pg 1684 Pg 1685
|
Question and Answers Forum |
AllQuestion and Answers: Page 1681 |
| let A = arctanx −arctany give another form of A if xy≠−1 . |
| let A = ∫_(−∞) ^(+∞) (dx/(x^2 −j)) with j=e^(i((2π)/3)) extract ReA and Im(A) and calculste its values. |
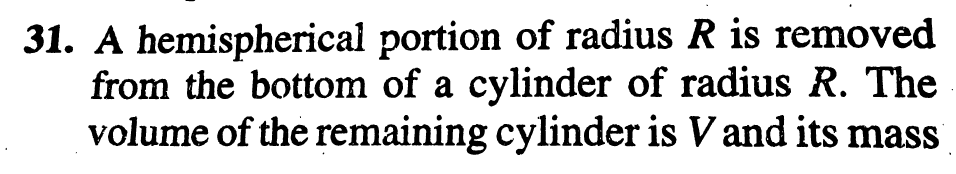
|
| Prove that (((n^2 )!)/((n!)^(n+1) )) is always an integer for n∈N. |
| what is the value of (√(5(√(5(√(5(√(5(√(5(√5))))))))))) ignoring 64. |
| p,q∈P m,n∈{0,1,2,...} How many pairs are there,whose LCM is p^m q^(n ) ,when: (i)(a,b) & (b,a) are considered same. (ii)(a,b) & (b,a) are considered different. (Generalization of Q# 34358) |
| how do i prove ∫_o ^t cos 2(ωt+α)dt=0 |
| How to do A4 size page layout in equation editor ? |
| The value of lim_(x→(π/2)) (([(x/2)])/(log (sin x))) = ? [.]= greatest integer function. |
| lim_(x→1) {1−x+[x−1]+[1−x]} = ? [.]= greatest integer function. |
| Determine number of possible pairs,whose GCD is 144 in case: (i) when (a,b) and (b,a) is considerd same. (ii) when (a,b) and (b,a) is considerd different. |
| Evaluate lim_(n→∞) ((n/(n^2 +1^2 ))+(n/(n^2 +2^2 ))+.....+(n/(n^2 +n^2 ))). |
| if a>b>0 prove that b<((ae^x +be^(−x) )/(e^x +e^(−x) ))<a |
| A right prism has a regular hexagonal base with sides of length 15cm,and a height of 20cm. find its volume and total surface area. |
| Determine number of possible pairs whose LCM is 144 in case, (i)when (a,b) & (b,a) are considered same. (ii)when(a,b) & (b,a) are considered different. |
| If a+b+c=0 prove that i)((a/(b+c))+ (b/(c+a)) +(c/(a+b)))(((b+c)/a) +((c+a)/b) +((a+b)/c))=9 ii)((a/(b−c)) +(b/(c−a)) +(c/(a−b)))(((b−c)/a) +((c−a)/b) +((a−b)/c))=9 |
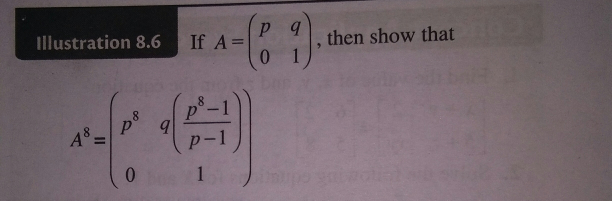
|
| a, b, c ∈ R, a≠0 and the quadratic equation ax^2 +bx+c=0 has no real roots, then |
| solve for x and y (i) 2^(x−1) .3^(y+1) =25 (ii)2^(n−1) .3^(m+1) =113 |
| calculate ∫_(−∞) ^(+∞) (dx/(x^2 +1 −i)) |
| find a eajivalent of u_n = ∫_0 ^∞ e^(−(t/n)) arcctant dt . |
| 1) find F(x)= ∫_0 ^(+∞) ((e^(−at) −e^(−bt) )/t)sin(xt)dt with a>0 ,b>0 . |
| let f(x)= ∫_0 ^(+∞) ((1−cos(xt))/t^2 ) e^(−t) dt calculate f(x) . |
| let u_0 =x ≠o and u_(n+1) =ln(((e^u_n −1)/u_n )) 1) study the convervence of (u_n ) 2)find Σ_(n=0) ^∞ (Π_(k=0) ^n u_k ) . |
| calculate I = ∫∫_D x^3 dxdy on the domain D ={(x,y)∈R^2 /1≤x≤2 , x^2 −y^2 −1≥0} |
| let give the d.e. (1+x^2 )y^(′′) +3xy^′ +y =0find a solution y(x) deveppable at integr serie with∣x∣<1 . |
Pg 1676 Pg 1677 Pg 1678 Pg 1679 Pg 1680 Pg 1681 Pg 1682 Pg 1683 Pg 1684 Pg 1685 |