
Question and Answers Forum
AllQuestion and Answers: Page 1787



Pg 1782 Pg 1783 Pg 1784 Pg 1785 Pg 1786 Pg 1787 Pg 1788 Pg 1789 Pg 1790 Pg 1791
|
Question and Answers Forum |
AllQuestion and Answers: Page 1787 |
| If x^2 + y^2 + 2xy + 2x + 2y + k = 0 represents pair of straight lines then find the value of k. |
| a two digit number is 3 more than 4 times the sum of its digits. if 18 is added to this number .the sum is equal to number obtained by interchanging the digits.find the number |
| ratio of income of two persons is 9 is to 7.ratio of their expenses is 4 is to 3 .every person saves rupees 200. find income of each. |

|
| There are 5 more girls than boys in a class. If 2 boys join the class, the ratio of girls to boys will be 5:4. Find the number of of girls in the class. |
| Prove that If f(x) is Riemann integrable on [a,b] and ∃M>0 s.t. ∀x∈[a,b] (f(x)≠0 and ∣f(x)∣<M and ∣(1/(f(x)))∣<M), then (1/(f(x))) is Riemann integrable on [a,b]. |
| 2000^(3000) vs 3000^(2000) who is stronger ? |
| Prove that b=2asin^2 θ ; when acosθ−bsinθ=c and θ=45° |
| find the value of (C_n ^(0 ) )^2 +(C_n ^1 )^2 +(C_n ^2 )^2 +...(C_n ^n )^2 . |
| let put S_n =Σ_(k=1) ^(k=n) (((−1)^k )/k) find S_(n ) in terms of H_n then lim_(n−>∝) S_n H_n = Σ_(k=1) ^(k=n) (1/k) ( harmonic serie) |
| y+2y^3 y^((1)) =(x+4yln (y))y^((1)) |
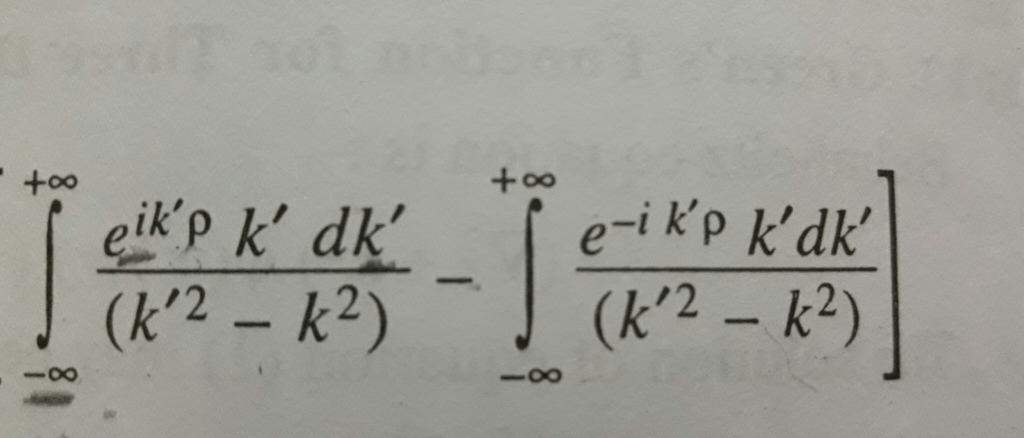
|
| answer to26109 S_n = Σ_(k=1) ^(k=n) (1/(k^2 (k+1)^2 )) we decompose F(X) = (1/(X^2 (X+1)^2 )) = (a/X) +(b/X^2^ ) +(c/(X+1)) +(d/((X+1)^2 )) we find F(X) = ((−2)/X) +(1/X^2 ) + (2/(X+1)) + (1/((X+1)^2 )) so S_n = −2Σ_(k=1) ^(k=n) (1/k) +2Σ_(k=1) ^(k=n) (1/(k+1)) +Σ_(k=1) ^(k=n) (1/k^2^ ) + Σ_(k=1) ^(k=n) (1/((k+1)^2 )) but Σ_(k=1) ^(k=n) (1/k) = H_n Σ_(k=1) ^(k=n) (1/(k+1))= H_(n+1) −1 Σ_(k=1) ^(k=n) (1/((k+1)^2 )) = Σ_(k=1) ^(k=n) (1/k^2 ) + (1/((n+1)^2 )) −1⇒ S_n = 2(H_(n+1) −H_n ) +2 Σ_(k=1) ^(k=n) (1/k^2 ) −3 but lim_(n−>∝) (H_(n+1) − H_n ) =0 and Σ_(k=1) ^∝ (1/k^2 ) = (π^2 /6) ⇒ lim_(n−>∝) S_n = 2 (π^2 /6) −3 = (π^2 /3) −3 . |
| (1/6)(√((3log1728)/(1+(1/2)log36+(1/3)log8))) simplify the question above |
| x^2 +(1/x^2 )=3 thrn find the valu of( x−(1/x))^2 |
| using 1st principle find the derivative of y=x^x |

|
| answer to 26024 let put c= ∫_0 ^∞ cos(ax^2 )dx and c = ∫_0 ^∞ sin(ax^2 )dx ew have c−is = ∫_0 ^∞ e^(−iax^2 ) dx =2^(−1) ∫_R e^(−iax^2 ) dx and i put x^(1/2) =r(x)(notation) so 2(c−is) = ∫_R e^(−(r(ia)x)^2 ) dx and by the changement t= r(ia) x we find 2(c+is) = (r(ia))^(−1) ∫_R e^(−t^2 ) dt = r(π)/r(ia) but r(ia) =r(i) r(a) = r(a) e^ −−>2(c+is) = r(π) r(a)^(−1) e^(−iπ/4) ^) −−> c = r(2π)/_(4r(a)) and s = r(2π)/_(4r(a)) |
| find the radius of convergence for the serie Σ_(n=1) ^∝ H_n x^n H_n = Σ_(k=1) ^(k=n) (1/k) . |
| let put ξ(x)= Σ_(n=1) ^∝ (1/n^x ) with x>1 and δ(x) =Σ_(n=1) ^∝ (((−1)^n )/n^x ) find a relation between ξ(x) and δ(x). |

|
| ∫((asin^3 θ+bcos^3 θ)/(sin^2 θ.cos^2 θ))dθ |
| Given f(x) = (1 − x + x^2 − x^3 + ... − x^(2015) + x^(2016) )^2 Find the sum of all odd coeffisiens! Ex. f(x) = (x^2 + x + 1)^2 = 1x^4 + 2x^3 + 3x^2 + 2x + 1 The sum of odd coeffisien is 1 + 3 = 4 |
| x^2 −x−42 factorise |
| solve the differential equation(D^2 +2D+1)y=x^2 +2x+1 |
| Find the value of ((2 + 3^2 )/(1! + 2! + 3! + 4!)) + ((3 + 4^2 )/(2! + 3! + 4! + 5!)) + ... + ((2013 + 2014^2 )/(2012! + 2013! + 2014! + 2015!)) |
Pg 1782 Pg 1783 Pg 1784 Pg 1785 Pg 1786 Pg 1787 Pg 1788 Pg 1789 Pg 1790 Pg 1791 |