
Question and Answers Forum
AllQuestion and Answers: Page 1807






Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811
|
Question and Answers Forum |
AllQuestion and Answers: Page 1807 |
| solve ∫tan^(−1) x ln (1+x^2 )dx |

|
| What is the answer for P(z=0.23)? |
| ∫sin(101x)sin^(99) xdx |
| ∫_1 ^2 x^3 +1=? |
| A function f is define by f : → 3 − 2sinx, for 0 ≤ x ≤ 360 find the range of f |

|
| (1+i)(2+i) |
| Why ΔS > 0 for the reaction 2HgO(s) → 2Hg(l) + O_2 (g)? |
| A certain ideal gas has C_(v, m) = a + bT, where a = 25 J/(mol. K) and b = 0.03 J(mol.K^2 ). Let 2 mole of this gas go from 300 K and 2 litre volume to 600 K and 4 litre. ΔS_(gas) is |
| Two blocks A and B of mass 1 kg and 2 kg respectively are connected by a string, passing over a light frictionless pulley. Both the blocks are resting on a horizontal floor and the pulley is held such that string remains just taut. At time t = 0, a force F = 20t N, starts acting on the pulley along vertically upward direction. Calculate vertical displacement of the pulley upto the instant when B loses contact with the floor. |
| A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1 rad/s. The spot of light P moves along the wall at a distance 3 m. What is the velocity of the spot P when θ = 45°? |
| If (1 − x^3 )^n = Σ_(r=0) ^n a_r x^r (1 − x)^(3n−2r) , then the value of a_r , where n ∈ N is (1)^n C_r ∙3^r (2)^n C_(3r) (3)^n C_(r−1) 2^(r−1) (4)^n C_r 2^r |
| Calculate the lattice enthalpy of MgBr_2 . Given that Enthalpy of formation of MgBr_2 = −524 kJ mol^(−1) Sublimation energy of Mg = +2187 kJ mol^(−1) Vaporisation energy of Br_2 (l) = +31 kJ mol^(−1) Dissociation energy of Br_2 (g) = +193 kJ mol^(−1) Electron gain enthalpy of Br = −331 kJ mol^(−1) |
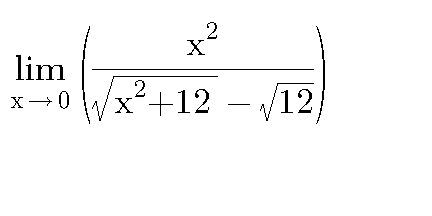
|
| Solve for x, y and z x^2 − yz = 1 .......... (i) y^2 − xz = 4 .......... (i) z^2 − xy = 9 .......... (i) |
| A function f is defined by f : x → 3 − 2sin(x), for 0 ≤ x ≤ 360° find the range of f |

|

|

|
| 5(tan^2 x−cos^2 x)=2cosx+a then find then find the value of cos4x.??? |

|
| A uniform rope of length L and mass per unit λ having one end fixed with the ceiling is released from rest. Find the tension in the fixed end as a function of the distance travelled by the movable end. |
| solve lim_(x→inf+) ∫^(2(√x)) _(2sin(1/x)) ((2t^4 +1)/((t−3)(t^3 +3))) dt |
| solve ∫^1_ _(−1) x^2 d(lnx) |
| Mr.Ajfour ,which app do you use for making these diagrams? |
Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 |