
Question and Answers Forum
AllQuestion and Answers: Page 1808




Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812
|
Question and Answers Forum |
AllQuestion and Answers: Page 1808 |

|
| A ball of mass 1 kg moving with velocity 3 m/s collides with spring of natural length 2 m and force constant 144 N/m. What will be length of compressed spring? |

|
| A rectangular wire frame ABCD is in vertical plane is moving with a constant acceleration a into the plane. Direction of gravity is shown in figure. A collar can move on wire AC of length l. Coefficient of friction between wire and collar is μ. Find (i) The minimum acceleration a so that collar does not slip on wire. (ii) The time taken by collar to reach C if acceleration is half the value calculated in part (i) |
| area of a(1−cos θ) |
| (1/(cos (x−a)cos (x−b))) |
| Which of the diagrams represents variation of total mechanical energy of a pendulum oscillating in air as function of time? |
| Common solution. (d/dy)(u_x +u)+2x^2 y(u_x +u)=0. |
| Find the value of x, ∫_(−∞) ^x dx = ∫∣± sinh cot ln (15−(√(33+x)))∣ dx |
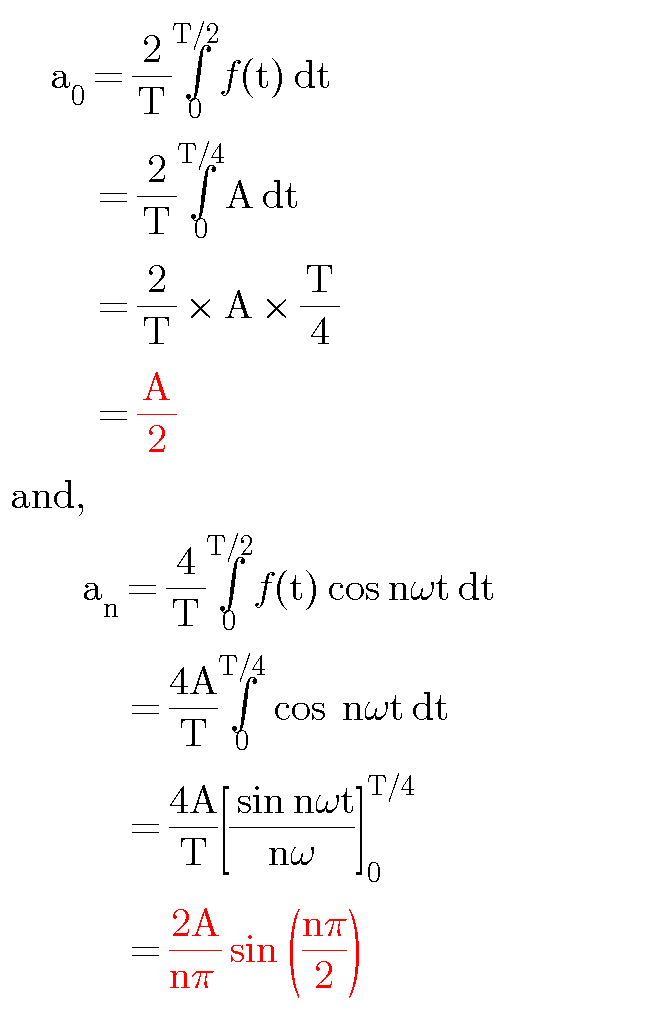
|

|
| Prove that ΣΣ_(0≤i<j≤n) ((1/(^n C_i )) + (1/(^n C_j ))) = Σ_(r=0) ^(n−1) ((n − r)/(^n C_r )) + Σ_(r=1) ^n (r/(^n C_r )) |

|
| Solve the equation: (∂^2 u/(∂x∂y)) = sin(x)cos(y), subjected to the boundary conditions at y = (π/2), (∂u/∂x) = 2x and x = π, u = 2sin(y) |

|
| Find a unit vector which is perpendicula to a vector A(3coma5coma1) Sorry for writing coma cuz i dnt see a key for it |
| ∫_0 ^∞ X^6 e^(−x/2) dx= |
| ∫_0 ^a f(x)dx= |
| If X is a discrete random variable then p(X≥a)= |
| An asymptote to the curve y^2 (1+x)=x^2 (1−x) is |
| the curve ay^2 =x^2 (3a−x) cuts the y-axis at |
| just a silly question: write a correct maths equation using only symbols below. Each must be used and only once. 2, 3, 4, 5, =, + |
| a,b,c>0 ⇒((a^3 +b^3 +c^3 )/((a+b)(b+c)(c+a)))≥(3/8) ? |
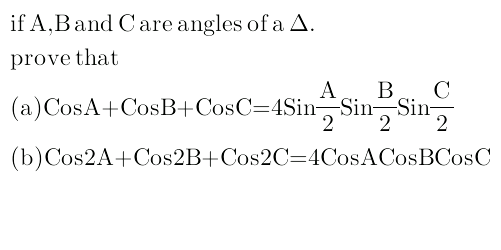
|
| ∫sec^2 (√x) /(√x) dx |

|
Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812 |