
Question and Answers Forum
AllQuestion and Answers: Page 1815





Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819
|
Question and Answers Forum |
AllQuestion and Answers: Page 1815 |
| If (1 + x)^n = C_0 + C_1 x + C_2 x^2 + C_3 x^3 + ... + C_n x^n , prove that (2^2 /(1.2))C_0 + (2^3 /(2.3))C_1 + (2^4 /(3.4))C_2 + ... + (2^(n+2) /((n + 1)(n + 2)))C_n = ((3^(n+2) − 2n − 5)/((n + 1)(n + 2))) |
| With usual notation, show that (C_0 /x) − (C_1 /(x+1)) + (C_2 /(x+2)) − .... + (−1)^n (C_n /(x+n))= ((n!)/(x(x + 1)(x + 2)....(x + n))) |
| ∫((2sinx+3cosx)/(3sinx+4cosx)) dx |

|
| Wow guys. You people are amazing.Its my pleasure to be a part of this forum. :) |
| ΔH_f ^o of water is −285.8 kJ mol^(−1) . If enthalpy of neutralization of monoacid strong base is −57.3 kJ mol^(−1) , ΔH_f ^o of OH^− ion will be |

|
| In the binomial expasion of (a − b)^5 , the sum of 2^(nd) and 3^(rd) term is zero, then (a/b) is |
| A chain consisting of 5 links each of mass 0.1 kg is lifted vertically with a constant acceleration of 2 m/s^2 . The force of interaction (in newton) between the top link and the link immediately below it will be : Take g = 10 m/s^2 . |

|
| The system is initially at origin and is moving with a velocity (3 m/s) k^∧ . A force (120t newton) i^∧ acts on mass m_2 , where t is time in seconds. The man throws a light ball, at the instant when m_1 starts slipping on m_2 , with a velocity 5 m/s vertically up w.r.t himself. Taking the masses of blocks and man as 60 kg each and assuming that the man never slips on m_2 , find (a) The time at which man throws the ball and (b) The coordinates of the point where ball lands. Neglect the dimensions of the system. (g = 10 m/s^2 ) |
| solve∫_0 ^1 ln(x)dx/x^2 −x−1 dx |
| Solve for all integer x,y ∈Z x^2 +y^2 =19 |
| If α = (5/(2!3)) + ((5.7)/(3!3^2 )) + ((5.7.9)/(4!3^3 )) ,... then find the value of α^2 + 4α. |
| ∫(x^(1/2) /(x^(1/2) −x^(1/3) ))dx= |
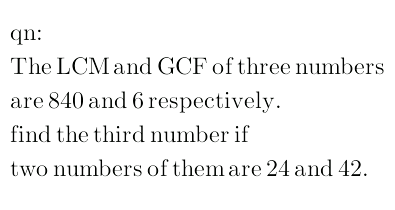
|
| Mr. Ajfour, you are very good at solving difficult questions.How do you do that ? Please tell us something about yourself. |
| show that (((a+b+c)^2 )/(a^2 +b^2 +c^2 ))= ((cot (1/2)A+cot (1/2)B+cot (1/2)C)/(cot A+cot B+cot C)) please help |
| How to solve this homogeneous equation. Can u help me plz Q. solve (x sin (y/x))dy −(y sin^(−1) (y/x))dx=0 |

|
| toutes lessolutions du systeme |
| Happy Diwali Friends !! :) |

|
| Find the coefficient of x in the expansion of [(√(1 + x^2 )) − x]^(−1) in ascending power of x when ∣x∣ < 1. |
| toutes les solutions ? |
| In a quadrilateral ABCD, it is given that AB is parallel to CD and the diagonals AC and BD are perpendicular to each other. Show that (a) AD.BC ≥ AB.CD; (b) AD + BC ≥ AB + CD. |
Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819 |