
Question and Answers Forum
AllQuestion and Answers: Page 1816





Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819 Pg 1820
|
Question and Answers Forum |
AllQuestion and Answers: Page 1816 |
| solve∫_0 ^1 ln(x)dx/x^2 −x−1 dx |
| Solve for all integer x,y ∈Z x^2 +y^2 =19 |
| If α = (5/(2!3)) + ((5.7)/(3!3^2 )) + ((5.7.9)/(4!3^3 )) ,... then find the value of α^2 + 4α. |
| ∫(x^(1/2) /(x^(1/2) −x^(1/3) ))dx= |
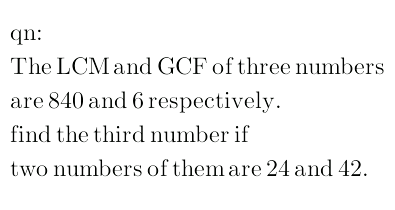
|
| Mr. Ajfour, you are very good at solving difficult questions.How do you do that ? Please tell us something about yourself. |
| show that (((a+b+c)^2 )/(a^2 +b^2 +c^2 ))= ((cot (1/2)A+cot (1/2)B+cot (1/2)C)/(cot A+cot B+cot C)) please help |
| How to solve this homogeneous equation. Can u help me plz Q. solve (x sin (y/x))dy −(y sin^(−1) (y/x))dx=0 |

|
| toutes lessolutions du systeme |
| Happy Diwali Friends !! :) |

|
| Find the coefficient of x in the expansion of [(√(1 + x^2 )) − x]^(−1) in ascending power of x when ∣x∣ < 1. |
| toutes les solutions ? |
| In a quadrilateral ABCD, it is given that AB is parallel to CD and the diagonals AC and BD are perpendicular to each other. Show that (a) AD.BC ≥ AB.CD; (b) AD + BC ≥ AB + CD. |
| If (a + bx)^(−2) = (1/4) − 3x + ..., then (a, b) = |
| A cylinder of weight 200 N is supported on a smooth horizontal plane by a light cord AC and pulled with force of 400 N. The normal reaction at B is equal to |
| A ball of mass 400 g travels horizontally along the ground and collides with a wall. The velocity-time graph below represents the motion of the ball for the first 1.2 seconds. The magnitude of average force between the ball and the wall is |
| The coefficient of x^r in the expansion of (1 − 2x)^(−1/2) is (1) (((2r)!)/((r!)^2 )) (2) (((2r)!)/(2^r (r!)^2 )) (3) (((2r)!)/((r!)^2 2^(2r) )) (4) (((2r)!)/(2^r (r + 1)!(r − 1)!)) |

|
| Predict the density of Cs from the density of the following elements K 0.86 g/cm^3 Ca 1.548 g/cm^3 Sc 2.991 g/cm^3 Rb 1.532 g/cm^3 Sr 2.68 g/cm^3 Y 4.34 g/cm^3 Cs ? Ba 3.51 g/cm^3 La 6.16 g/cm^3 |

|
| A ladder of mass m is leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ_1 and that between the floor and the ladder is μ_2 . The normal reaction of the wall on the ladder is N_1 and that of the floor is N_2 . If the ladder is about to slip, then (1) μ_1 = 0, μ_2 ≠ 0 and N_2 tan θ = mg/2 (2) μ_1 ≠ 0, μ_2 = 0 and N_1 tan θ = mg/2 (3) μ_1 ≠ 0, μ_2 ≠ 0 and N_2 = ((mg)/(1 + μ_1 μ_2 )) (4) μ_1 = 0, μ_2 ≠ 0 and N_1 tan θ = ((mg)/2) |
| { ((x+y^2 +z^3 =3)),((y+z^2 +x^3 =3)),((z+x^2 +z^3 =3)) :} trouver les solutions positives |
| A force F^→ = 2xj^∧ newton acts in a region where a particle moves anticlockwise in a square loop of 2 m in x-y plane. Calculate the total amount of work done. Is this force a conservative force or a non-conservative force? |

|
Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819 Pg 1820 |