
Question and Answers Forum
AllQuestion and Answers: Page 1853


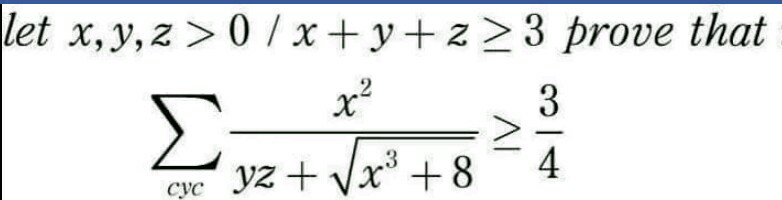



Pg 1848 Pg 1849 Pg 1850 Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857
|
Question and Answers Forum |
AllQuestion and Answers: Page 1853 |

|
| ∫(√(1+x^4 )) dx please solve this question. |
| x − 5x + 3 = 7 −4x = 4 x = −1 |
| x−5×+3=7 |
| Argon diffuses through a hole under prescribed condition of temperature and pressure at the rate of 3cm^3 per velocity. At what velocity will helium diffuse through the same hole under the same condition (Ar = 29.94 g, He = 4g). |
| lim_(x→0) (((sin x)/x))^((sin x)/(x−sin x)) |

|
| A block of mass M is pulled vertically upward through a rope of mass m by applying force F on-one end of the rope. What force does the rope exert on the block? |
| (1/3)+(3/(3×7))+(5/(3×7×11))+(7/(3×7×11×15))+...n terms |
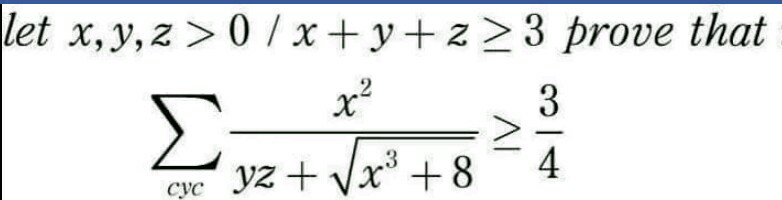
|
| The work function of a metal is 4 eV. If light of frequency 2.3 × 10^(15) Hz is incident on metal surface, then, (1) No photoelectron will be ejected (2) 2 photoelectron of zero kinetic energy are ejected (3) 1 photoelectron of zero kinetic energy is ejected (4) 1 photoelectron is ejected, which required the stopping potential of 5.52 volt |
| Without using L Hospital′s rule prove that lim_(x→0) ((sin x)/x)=1 |

|
| ∫ ((sin x)/(1 + cos^2 x)) dx |
| sin x = ((2a + 3)/(a + 1)) How many a that can satisfy the equation above? |
| lim_(x→0) ((x . tan x)/(x sin x − cos x + 1)) |
| Prove sin (((3π)/(10)))=((1+(√5))/4) |
| If ( ) represents the least integer function, then the value of (10) + (10 + (1/(20))) + (10 + (2/(20))) + ... + (10 + ((19)/(20))) is equal to (1) 219 (2) 200 (3) 220 (4) 221 |
| The maximum value of f(x) = 2 − ∣x∣^2 − 2x is equal to (1) 6 (2) 4 (3) 5 (4) 3 |
| The energy required to dislodge electron from excited isolated H-atom, IE_1 = 13.6 eV is (1) = 13.6 eV (2) > 13.6 eV (3) < 13.6 eV and > 3.4 eV (4) ≤ 3.4 eV |
| In moving a body of mass m up and down a rough incline plane of inclination θ, work done is (S is length of the planck, and μ is coefficient of friction). |
| The acceleration of an object is given by a(t) = cos(nπ), and its velocity at time t = 0 is (1/(2π)). Find both the net and the total distance traveled in the first 1.5 seconds. |

|
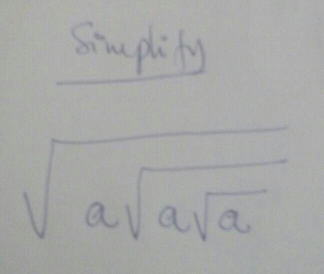
|

|
| A particle of mass 1 gram executes an oscillatory motion on the concave surface of a spherical dish of radius 2 m, placed on a horizontal plane. If the motion of the particle starts from a point on the dish at the height of 1 cm from the horizontal plane and the coefficient of friction is 0.01, how much total distance will be moved by the particle before it comes to rest? |
Pg 1848 Pg 1849 Pg 1850 Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 |