
Question and Answers Forum
AllQuestion and Answers: Page 1856








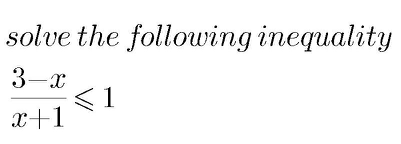


Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 Pg 1858 Pg 1859 Pg 1860
|
Question and Answers Forum |
AllQuestion and Answers: Page 1856 |
| Let a, b, c ∈ R, a ≠ 0, such that a and 4a + 3b + 2c have the same sign. Show that the equation ax^2 + bx + c = 0 can not have both roots in the interval (1, 2). |
| A river of width d is flowing with speed u as shown in the figure. John can swim with maximum speed v relative to the river and can cross it in shortest time T. John starts at A. B is the point directly opposite to A on the other bank of the river. If t be the time John takes to reach the opposite bank, match the situation in the column I to the possibilities in column II. Column I (A) John reaches to the left of B (B) John reaches to the right of B (C) John reaches the point B (D) John drifts along the bank while minimizing the time Column II (p) t = T (q) t > T (r) u < v (s) u > v |

|
| N propositions are judged by 2k−1 people. Each person assigns “true” to exactly M propositions and “false” to the other N−M (M ≤ N). To say a proposition is “approved” means it is true according to at least k judges. Find the minimum and maximum numbers of approved propositions given N, M and k. |
| Suppose one is given two vector field A and B in region of space such that, A(x,y,z) = 4xi + zj + y^2 z^2 k B(x,y,z) = yi +3j − yzk Find: C(x,y,z) if C = A ∧ B Also prove that, C(x,y,z) is perpendicular to A(x,y,z) |
| Let ABC and ABC′ be two non- congruent triangles with sides AB = 4, AC = AC′ = 2(√2) and angle B = 30°. The absolute value of the difference between the areas of these triangles is |
| From the topic transformer prove that: e = (√2) ε cos(ωt) |

|
| Consider the iteration x_(k+1) =x_k −(([f(x)]^2 )/(f(x_k +f(x_k ))−f(x_k ))), k=0,1,2,... for the solution of f(x)=0. Explain the connection with Newton′s method, and show that (x_k ) converges quadratically if x_0 is sufficiently close to the solution. |

|
| y=tan x^(tan x^(tan x) ) |
| Prove that a^4 + b^4 + c^4 ≥ abc(a + b + c) |

|

|

|

|

|

|
| Find Z_x and Z_y for each of the functions below (a) Z = 8x^2 y + 14xy^2 + 5y^2 x^3 (b) Z = 4x^3 y^2 + 2x^2 y^3 − 7xy^5 |
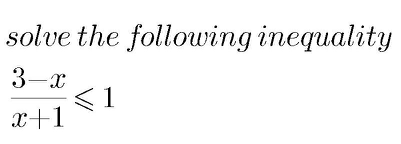
|
| Σ((cos 2rθ)/(sin^2 2rθ−sin^2 θ)) |
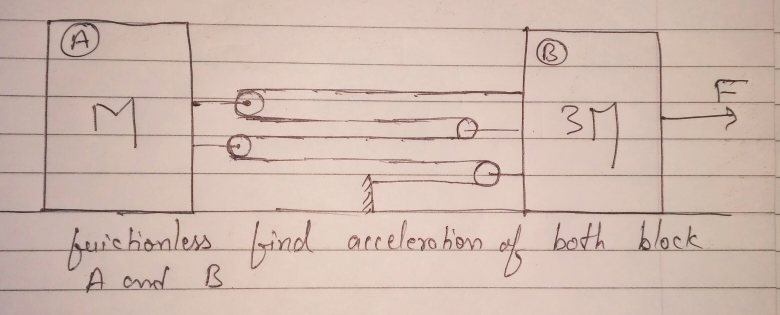
| The pulley arrangements are identical. The mass of the rope is negligible. In (a), the mass m is lifted up by attaching a mass (2m) to the other end of the rope. In (b), m is lifted up by pulling the other end of the rope with a constant downward force F = 2mg. In which case, the acceleration of m is more? |
| ∫ ((x + sinx)/(cosx)) dx |

|

|
| In a triangle ABC with fixed base BC, the vertex A moves such that cos B + cos C = 4 sin^2 (A/2) . If a, b and c denote the lengths of the sides of the triangle opposite to the angles A, B and C respectively, then (1) b + c = 4a (2) b + c = 2a (3) Locus of point A is an ellipse (4) Locus of point A is a pair of straight lines |
Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 Pg 1858 Pg 1859 Pg 1860 |