
Question and Answers Forum
AllQuestion and Answers: Page 1857

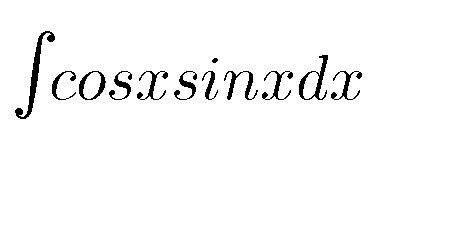
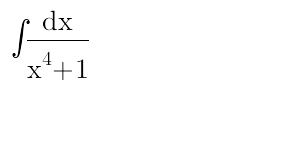

Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 Pg 1858 Pg 1859 Pg 1860 Pg 1861
|
Question and Answers Forum |
AllQuestion and Answers: Page 1857 |
| If cos^2 x_1 + cos^2 x_2 + cos^2 x_3 + cos^2 x_4 + cos^2 x_5 = 5, then sin x_1 + 2sin x_2 + 3sin x_3 + 4sin x_4 + 5sin x_5 is less than or equal to |
| x^x^x = 2, find x |
| Find the partial derivatives for each of the following (a) Z = 3x^2 (5x + 7y)^2 (b) Z = (w − x − y)^2 (3w + 2x − 4y) |

|
| ∫_0 ^5 (1/(∫_1 ^8 e^x^(−5) ))dx |
| If k is any possible number. what is the size of angle between the vectors a(K, k) and b(− 3, 4) |
| Given: x^2 + y^2 Show that, (d^2 y/dx^2 ) = ((xy)/(y^2 + x^2 )) |
| Two trains 150 m long and 250 m long are travelling at the speed of 30 kmph and 33 kmph respectively on parallel tracks in opposite directions. What is the time taken by these trains to cross each other completely from the moment they meet? |
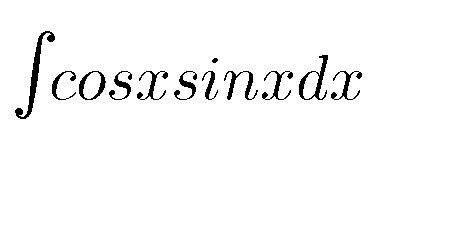
|
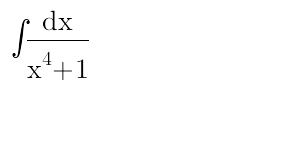
|
| In an 1800 m race, P beats Q by 50 seconds. In the same race, Q beats R by 40 seconds. If P beats R by 450 m, by what distance does P beat Q ?(in m) |
| A balloon moves up vertically such that if a stone is projected with a horizontal velocity u relative to balloon, the stone always hits the ground at a fixed point at a distance ((2u^2 )/g) horizontally away from it. Find the height of the balloon as a function of time. |
| There are two parallel planes, each inclined to the horizontal at an angle θ. A particle is projected from a point mid way between the foot of the two planes so that it grazes one of the planes and strikes the other at right angle. Find the angle of projection of the projectile. |
| The flow velocity of a river increases linearly with the distance (r) from its bank and has its maximum value v_0 in the middle of the river. The velocity near the bank is zero. A boat which can move with speed u in still water moves in the river in such a way that it is always perpendicular to the flow of current. Find (i) The distance along the bank through which boat is carried away by the flow current, when the boat crosses the river. (ii) The equation of trajectory for the coordinate system shown. Assume that the swimmer starts from origin. |
| A balloon starts rising from the surface of earth. The ascension rate is constant and is equal to v_0 . Due to wind the balloon gathers horizontal velocity component v_x = ay, where a is a positive constant and y is the height of ascent. Find (i) The horizontal drift of the balloon x(y), (ii) The total, tangential and normal accelerations of the balloon. |
| Two swimmers leave point A on one bank of the river to reach point B lying right across the other bank. One of them crosses the river along the straight line AB while the other swims at right angle to the stream and then walks the distance that he has been carried away by the stream to get to point B. What was the velocity v of his walking if both swimmers reached the destination simultaneously? (The stream velocity v_0 = 2 km/h and the velocity v′ of each swimmer with respect to still water is 2.5 km/h). |
| A particle is projected at an angle 60° with speed 10(√3) m/s from the point A as shown in the figure. At the same time the wedge is made to move with speed 10(√3) m/s toward right as shown in figure. Find the time after which particle will strike the wedge. |
| A sky diver of mass m drops out with an initial velocity v_0 = 0. Find the law by which the sky diver′s speed varies before the parachute is opened if the drag is proportional to the sky diver′s speed. Also solve the problem when the sky diver′s initial velocity has horizontal component v_0 and vertical component zero. |
| A point P is located above an inclined plane. It is possible to reach the plane by sliding under gravity down a straight frictionless wire joining to some point P ′ on the plane. How should P ′ be chosen so as to minimize the time taken? |
| (((x+1)(x−1))/(x^2 +2x+3)) |

|
| ∫ (dx/(1 − sin x + cos x)) |
| If y = (√(x^2 + (√(x^2 + (√(x^2 + (√(...)))))))) find ∫(y + (√y)) dx |
| If f(x) = (√(x^2 (√(3(√(x^2 (√(3(√)...)))))))) find ∫ f(x) dx |
| ∫cos2x ln(1+tanx)dx |
| prove that ∫_0 ^( π) ((x tanx)/(tanx+secx))dx=(π/2)(π−2) |
Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 Pg 1858 Pg 1859 Pg 1860 Pg 1861 |