
Question and Answers Forum
AllQuestion and Answers: Page 1892




Pg 1887 Pg 1888 Pg 1889 Pg 1890 Pg 1891 Pg 1892 Pg 1893 Pg 1894 Pg 1895 Pg 1896
|
Question and Answers Forum |
AllQuestion and Answers: Page 1892 |
| (1/7)=.142857^(−) (1/7) is a recurring decimal of period 6. What will be the period of (1/7^(20) )? |
| Expansion of 1000! has 249, 0′s at the end Find the first non−zero digit from right. 1000!=......d000...00 What is the value of d? |
| what is NBS? |
| The volume of a right circular cone is 5 litres . Calculate the volumes of the two parts into which the cone is divided by a plane parallel to the base , One third of the way down from the vertex to the base. Give your answer to the nearest ml. |
| Assuming no air resistance, and angle of projection α=(π/4) , find the ratio of the length of trajectory L of a projectile motion (by the time it hits the ground) to its horizontal range R on ground. (L/R)=? |
| Volume of a bubble is 3 times larger when it reaches the surface from the bottom of the lake. What is the depth of the lake? (A) 10 m (D) 40 m (B) 20 m (E) 50 m (C) 30 m |

|
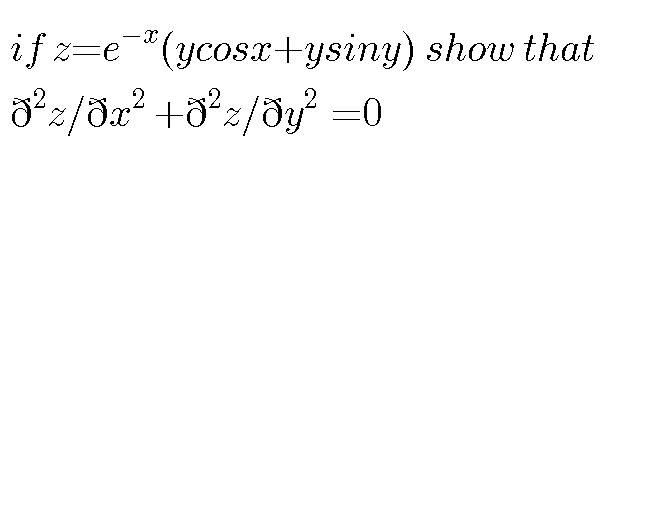
|

|
| Prove that cos^2 x + cos^2 3x + cos^2 5x + ... to n terms = (1/2)[n + ((sin4nx)/(2sin2x))] |
| The sum of the series sinθ + sin(((n − 4)/(n − 2)))θ + sin(((n − 6)/(n − 2)))θ + ... n terms is equal to (1) sin(((nθ)/(2 − n))) (2) cos(((2nθ)/(2 − n))) (3) tannθ (4) cotnθ |
| 2xyy′+(x−1)y^2 =x^2 e^x |
| x^2 +y^2 =5.....(1) 3x^2 +xy+y^2 =1.....(2) please help find x and y |
| please is factor theorem and error and trial the same? please help cause i think theres a difference but i cant explain it. Thankz. |
| A steam envine of efficiency 70% burns 20g of coal to produce 10kJ of energy.If it burns 200g of coal per second,calculate its output power. |

|
| Prove that cosech^(−1) (x) = sinh^(−1) ((1/x)) |

|
| if distance is given by x(t)=2t+5 then ,the acceleration at 4s is............ |
| Show that 19^(93) − 13^(99) is a positive integer divisible by 162. |
| Sum the following: tan x+2tan 2x+2^2 tan 2^2 x+...+2^n tan 2^n x |
| Let f : R − {(3/5)} → R be defined by f(x) = ((3x + 2)/(5x − 3)) . Then, (a) f^(−1) (x) = x (b) f^(−1) (x) = −f(x) (c) fof(x) = −x (d) f^(−1) (x) = (1/(19))f(x) |
| Evaluate: ∫_0 ^(2π) e^(x/2) sin ((x/2) + (π/4))dx |
| Evaluate: ∫_0 ^(2π) e^x cos ((π/4) + (x/2))dx |
| If g(x) = x^2 + x − 2 and (1/2) gof(x) = 2x^2 − 5x + 2, then prove that f(x) = 2x − 3. |
| If f : R → (−1, 1) is defined by f(x) = ((−x∣x∣)/(1 + x^2 )) , then prove that f^(−1) (x) = −sgn(x)(√((∣x∣)/(1 − ∣x∣))) |
Pg 1887 Pg 1888 Pg 1889 Pg 1890 Pg 1891 Pg 1892 Pg 1893 Pg 1894 Pg 1895 Pg 1896 |