
Question and Answers Forum
AllQuestion and Answers: Page 1904


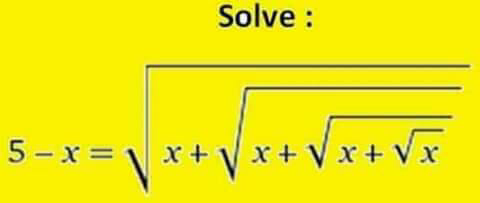

Pg 1899 Pg 1900 Pg 1901 Pg 1902 Pg 1903 Pg 1904 Pg 1905 Pg 1906 Pg 1907 Pg 1908
|
Question and Answers Forum |
AllQuestion and Answers: Page 1904 |
| Solve the differential equation (dy/dx) = ((4x + 2y − 3)/(8x − 4y + 5)) |
| Solve the differential equation (dy/dx) = ((2xy)/(x^2 + y^2 )) |
| Find the nth term of this sequence 3, 18, 45, 84, 135 ... |
| 5!! = ? |
| For all n ≥ 1 , n ∈ Z, prove that, p(n) : 4 + 8 + ... + 4n = 2n(n + 1) |
| Multi−point ∮(x)=x^3 well be equal to the values of the function ant its harvest. |

|
| Show that, 0.9999999999999 ...... ∞ is equal to 1 |
| Find the fraction to the below deimal 4.4444444444444....... ∞ |
| A particle is moving with velocity v=K(yi^ +xj^ ) prove that y^2 =x^2 +constant |
| ∫(1/(sin(x)))dx |

|
| The value of xyz is 15/2 or 18/5 according as the series a,x,y,z,b are in an A.P. or H.P., then ′a+b′ equals where a, b are +ve integers. |
| Prove that ∀x∈[1,2] ⇒ 1−x^2 ≤ x |
| ∫x^2 ×sgn(2x)dx=? |
| In any △ABC, 2(bc cos A+ca cos B+ab cos C) = |
| If tan α equals the integral solution of the inequality 4x^2 −16x+15<0 and cos β equals to the slope of the bisector of the first quadrant, then sin (α+β) sin (α−β) is equal to |

|
| Two angles of a triangle are cot^(−1) 2 and cot^(−1) 3. Then the third angle is |
| If the ratio of the students that pass a test to those that fail is in ratio 4:1, If 9 students were chosen at random, what is the probability that exactly 7 passed the test. |
| Find the 35th derivative of (2x^3 + 5x^4 )^(60) |

|
| (1/(1+1^2 +1^4 ))+(2/(1+2^2 +2^4 ))+(3/(1+3^2 +3^4 ))+.....∞=? |
| ∫ sin(x^4 )cos(x^2 ) dx |
| Find the area of the region between the graphs of f(x) = 3x^3 − x^2 − 10x and g(x) = − x^3 + 2x |

|
Pg 1899 Pg 1900 Pg 1901 Pg 1902 Pg 1903 Pg 1904 Pg 1905 Pg 1906 Pg 1907 Pg 1908 |