
Question and Answers Forum
AllQuestion and Answers: Page 1943


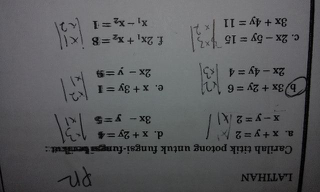






Pg 1938 Pg 1939 Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945 Pg 1946 Pg 1947
|
Question and Answers Forum |
AllQuestion and Answers: Page 1943 |
| (1^2 /(1×3))+(2^2 /(3×5))+...+((n2)/((2n−1)(2n+1)))=((n(n+1)/(2(2n+1))) |
| x_(1,1) =1 x_(n+1,m) =x_(n,m) +m x_(n,m+1) =nx_(n,m) −1 x_(2,2) =? |
| Evaluate the integral ∫[a(b^• .a + b.a^• ) + a^• (b.a) − 2(a^• .a)b − b^• ∣a∣^2 ]dt In which a^• ,b^• are the derivatives of a,b with respect to t |
| ∫cos x/4−x^2 ∫((cos x)/(4−x^2 )) |
| If z∈C satisfies ∣z^3 +z^(−3) ∣≤2 then maximum possible value of∣z+z^(−1) ∣is? |

|
| A balloon is inflated such that every point expands at a units/second. An ant runs from one point A to another point B. If the ant moves b units/second, what will influence if or not the ant will ever reach point B? |
| Find an integer x that satisfies the equation x^5 −101x^3 −999x^2 +100900=0 |
| Solving for A. U(z) = U_b +((2A)/(h+1))(ρ×g×sin(α))^n [H^(n+1) −(H−Z)^(n+1) ] |
| solving for B? U_b = U_s − (2/(n+1))(((ρ×g×sinα)/B))^n H^(n+1) |
| ∫_0 ^( ∞) x^(−ln(x)) dx |
| (((x−5)^(x^2 −11×−26) +(x−5)^(x^2 −171×+26) )/(x^2 +3x−203))=x . fine x. |
| Divide a circle in two equal parts by drawing an arc. |

|
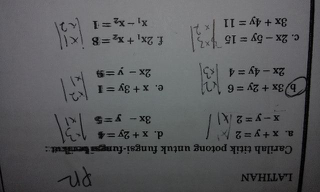
|

|
| ∫_0 ^∞ x.e^(−x^2 ) dx evaluate above expression. |

|

|
| if I=a(1−(r/(100)))^n make n the subject of formular |
| If the roots of 2x^2 +7x+5=0 are the reciprocal roots of ax^2 +bx+c=0, then a−c = ______. |
| p_n =n^(th) prime number p_1 =2, p_2 =3, p_3 = 5, ... Does the following converge: Σ_(i=1) ^∞ (p_i /p_(i+1) ) Prove/disprove |

|

|

|
| Write an expression involving e and π which when evaluated gives result 1. |
Pg 1938 Pg 1939 Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945 Pg 1946 Pg 1947 |