
Question and Answers Forum
AllQuestion and Answers: Page 1945



Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945 Pg 1946 Pg 1947 Pg 1948 Pg 1949
|
Question and Answers Forum |
AllQuestion and Answers: Page 1945 |

|
| 2×2 |
| p = ((a[1 − (1 + r)^(−n) ])/r) Make r the subject of the fomular. |
| (U_n )= 2,3,5,6,7,8,10,11,12,13,14,.... find U_n |
| (√4)+5 = |
| y^2 + x^2 = 2^x + 2^y Find the possible greatest value of ∣x − y∣ |

|

|
| Q. ∫((√(x^4 +1))/(x^2 −1)) dx |
| Find x_n (n∈Z) satisfying x_0 =0, x_1 =1 and x_(n+1) =x_n (√(x_(n−1) ^2 +1))+x_(n−1) (√(x_n ^2 +1)) for n≥1. |
| If a, b, c are in AP then (a/(bc)) , (1/c) , (2/b) are in |
| The sum of the squares of three distinct real numbers which are in GP is S^2 . If their sum is α S, then |
| If a, b, c are in AP; b, c, d are in GP and c, d, e are in HP, then a, c, e are in |
| If a, b, c are in AP; b, c, d are in GP and c, d, e are in HP, then a, c, e are in |
| If n Arithmetic means are inserted between two quantities a and b, then their sum is equal to |
| A (2 × 3) rectangle and a (3 × 4) rectangle are contain within a square without over laping at any inferior point , and the sides of the square are parallel to the sides of the two given rectangles. what is the smallest possible area of the square. |
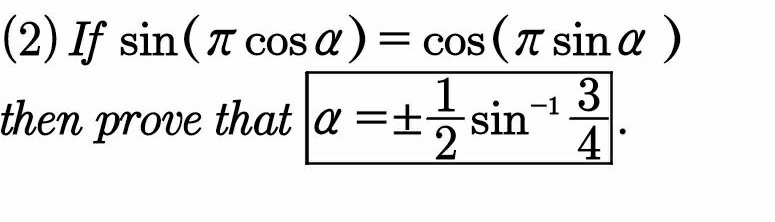
|
| Factorise the expression 9x^4 + (1/x^4 ) +2. |
| Factorise the expression 9x^4 + (1/x^4 ) +2. |
| Given r, t, j >0 and n≥1; Prove that (([Σ_(p_1 =1) ^n (p_1 ^r +r)+Σ_(p_2 =1) ^n (p_2 ^t +t)]^2 )/(n^2 [(n!)^((r+t)/n) +r(n!)^(t/n) +t(n!)^(r/n) +rt])) +(([Σ_(p_2 =1) ^n (p_2 ^t +t)+Σ_(p_3 =1) ^n (p_3 ^j +j)]^2 )/(n^2 [(n!)^((t+j)/n) +t(n!)^(j/n) +j(n!)^(t/n) +tj])) ≥ 8 By: Mr. Chheang Chantria |
| ∫{((1−(√x))/(1+(√x)))}^(1/2) (dx/x)=? |
| Compute lim_(A→+∞) {(1/A)∫_1 ^A A^(1/x) dx}. (IMC 2015) |
| Let E be a banach space , Y is normed space and suppose that {Ta : a∈A} ⊆ B (E, Y) If {Tax : a∈A} ⊆ Y is bounded , for all x∈E, then {∥Ta∥ : a∈A} is bounded. |
| 5^(√(x )) − 5^(x − 7) = 100 Find the value of x. x = 9 please workings. |
| A pen with a cylindrical barrel of diameter 2 cm and height 10.5 cm, filled with ink, can write 3300 words. How many words can be written with that pen using 100 ml of ink. (Take 1cc = 1 ml) |
| If A= [(1,2,3),(6,5,4) ] , then A^T =____. |
Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945 Pg 1946 Pg 1947 Pg 1948 Pg 1949 |