
Question and Answers Forum
AllQuestion and Answers: Page 1965
Pg 1960 Pg 1961 Pg 1962 Pg 1963 Pg 1964 Pg 1965 Pg 1966 Pg 1967 Pg 1968 Pg 1969
|
Question and Answers Forum |
AllQuestion and Answers: Page 1965 |
| ∫(1/(1+cot x))dx |
| Evaluate the integral. ∫[(x−(x^3 /2)+(x^5 /(2.4))−(x^7 /(2.4.6))+...)(1−(x^2 /2^2 )+(x^4 /(2^2 .4^2 ))−(x^6 /(2^2 .4^2 .6^2 ))+....)]dx for 0<x<∞ Please help |
| Find all positive integers n for which there exist non−negative integer . a_(1 ) a_2 a_3 ....... a_n . Such that (1/2^a_1 ) + (1/2^a_2 ) + (1/2^a_3 ) + .... + (1/2^a_n ) = (1/3^a_1 ) + (2/3^a_2 ) + .... + (n/3^a_n ) = 1 Please help. |

|
| ∫e^(−st) (t^n /(n!))dt=? |
| Prove that among all triangles, which have same circum-radius, the equilateral triangle has maximum area. |
| L=lim_(x→0) x^x |
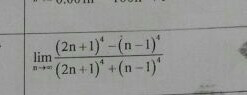
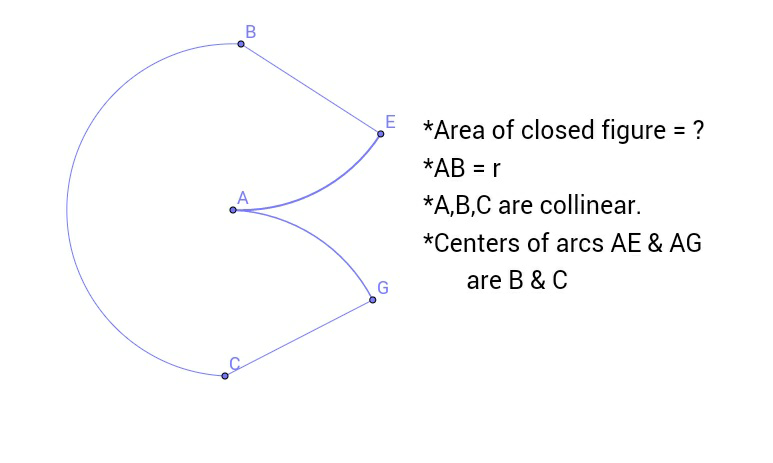
|
| Town A is 36 kilometers from town B. Two persons start to travel at the same time, one from A to B and other from B to A. After meeting in a way the first person covers the remaining distance in 2 hours and the second in 8 hours. Determine their speed. (From a book) |
| Solve simultaneously 2x + y − z = 8 ........... (i) x^2 − y^2 +2z^2 = 14 .......... (ii) 3x^3 + 4y^3 + z^3 = 195 ......... (iii) please help me. |
| ∫((cos2x)/(sin^2 x∙cos^2 x))dx |
| Prove that among all cyclic n-gons, which have same radius, regular n-gon has maximum area. |
| Please help me with that simultaneous equation |
| How many ways can you express 30,030 as the product of 4 positive numbers? (excluding 1) |
| Solve simultaneously 2x + y − z = 8 ...... equation(i) x^2 − y^2 + 2z^2 = 14 .... equation(ii) 3x^3 + 4x^3 + z^3 = 195 ..... equation(iii) please help thanks. |
| Solve simultaneously 2x + y − z = 8 ........... (i) x^2 − y^2 + 2z^2 = 14 .......... (ii) 3x^3 + 4y^3 + z^3 = 195 ........... (iii) Please help. though equation. Thanks for your help. |
| Determine: 1+((a+r)/(ar))+((a+2r)/(ar^2 ))+...+((a+(n−1)r)/(ar^(n−1) )) |
| Determine: a^a +(ar)^(a+r) +(ar^2 )^(a+2r) +...+(ar^(n−1) )^(a+(n−1)r) |
| Why x+x=2x ? Explain by properties/laws. |
| at developers can we please have capital greek symbols? It would make things so much better when writing functions <3 |
| ∃x∈Z^+ :x=p_1 p_2 ...p_n ∧∀p≠x, p∈Z^+ x=(factors of p_1 )(fact. p_2 )...(fact. p_n ) How could you formally write the number of ways you can write x in terms of the product of n integers? |
| The exponent of 12 in 100! is |
| q+ |
| Find to the nearest hundredth the positive cube-root of 29 . |
| (√((x−1)/(3x+2))) + 2 ((√((3x+2)/(x−1))) ) = 3 Find the value of x |
| 2^x = 4x Solution 2^x = 4x This can be re write as (1+1)^x = 4x Using combination to epand from the identity. (1+x)^n = 1+nx+((n(n−1))/(2!))x^2 +((n(n−1)(n−2))/(3!))x^3 +....+nCrx^(r ) Therefore. (1+1)^x = 4x 1+x+((x(x−1))/(2!))(1^2 )+((x(x−1)(x−2))/(3!))(1^3 )+......+1 = 4x ignore the continuity (what rule is ..... ignore the +...+) is it linear approximation 1+x+((x^2 −x)/(2×1))+(((x^2 −x)(x−2))/(3×2×1))+1 = 4x 1+x+((x^2 −x)/2)+((x^3 −2x^2 −x^2 +2x)/6)+1 = 4x 1+x+((x^2 −x)/2)+((x^3 −3x^2 +2x)/6)+1 = 4x Multiply through by 6 6+6x+3(x^2 −x)+x^3 −3x^2 +2x+6 = 24x 12+6x+3x^2 −3x+x^3 −3x^2 +2x+6 = 24x 12+5x+x^3 = 24x 12+5x+x^3 −24x = 0 x^3 −19x+12 = 0 Factorize x^3 −4x^2 +4x^2 −16x−3x+12 = 0 (x^3 −4x^2 )+(4x^2 −16x)−(3x+12) = 0 x^2 (x−4)+4x(x−4)−3(x−4) = 0 Factor out (x−4) (x−4)(x^2 +4x−3) = 0 x−4 = 0 or x^( 2) +4x−3 = 0 x = 4 or x = 0.6458 or x = −4.6458 The only real solution is x = 4 Therefore x = 4 DONE! Please confirm the solution. is it correct or please corect it or show me alternative. This is my trial. Thanks. |
Pg 1960 Pg 1961 Pg 1962 Pg 1963 Pg 1964 Pg 1965 Pg 1966 Pg 1967 Pg 1968 Pg 1969 |