
Question and Answers Forum
AllQuestion and Answers: Page 233


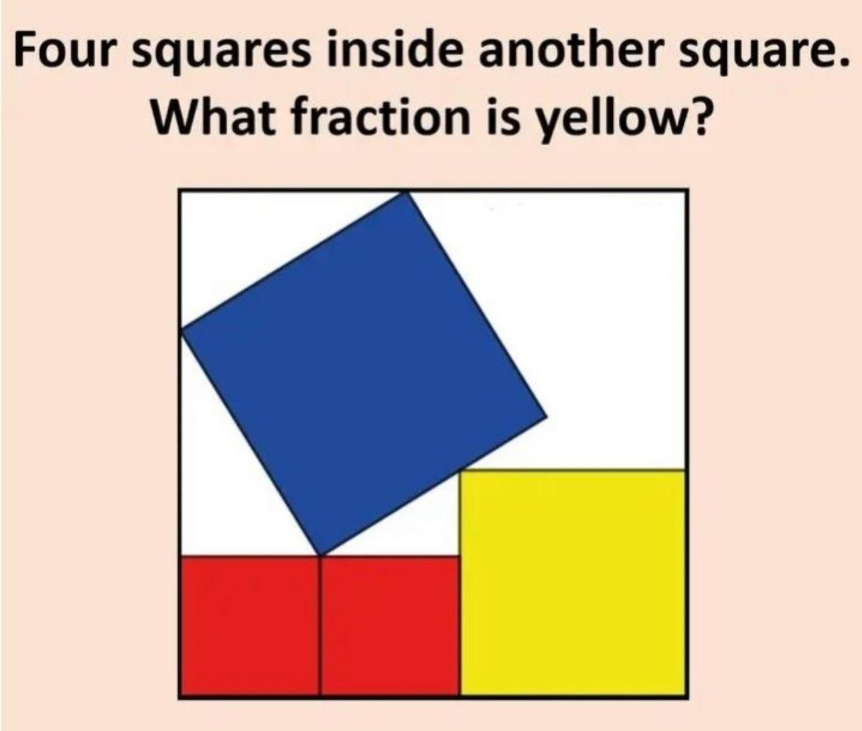
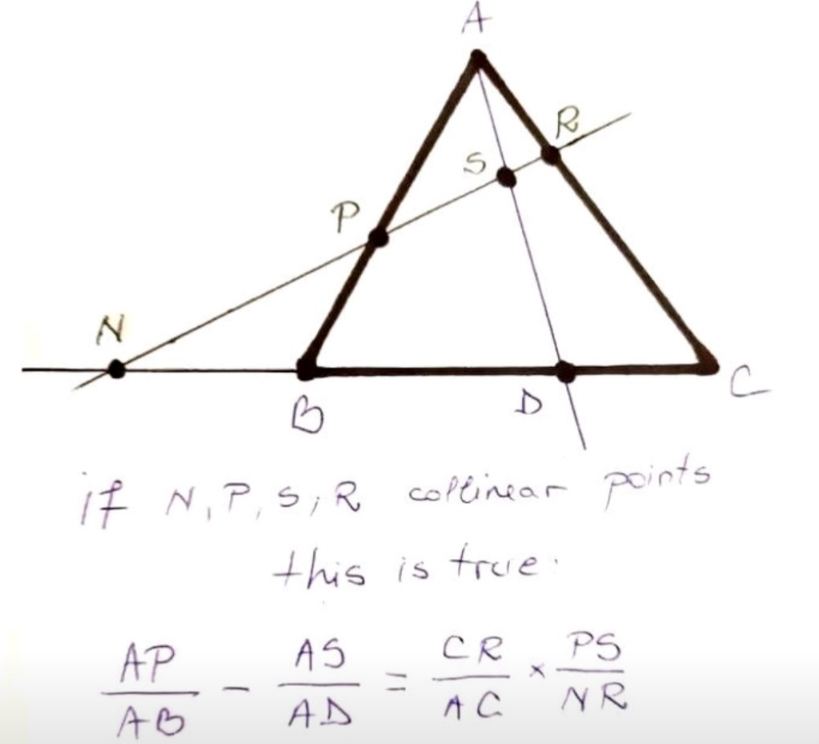




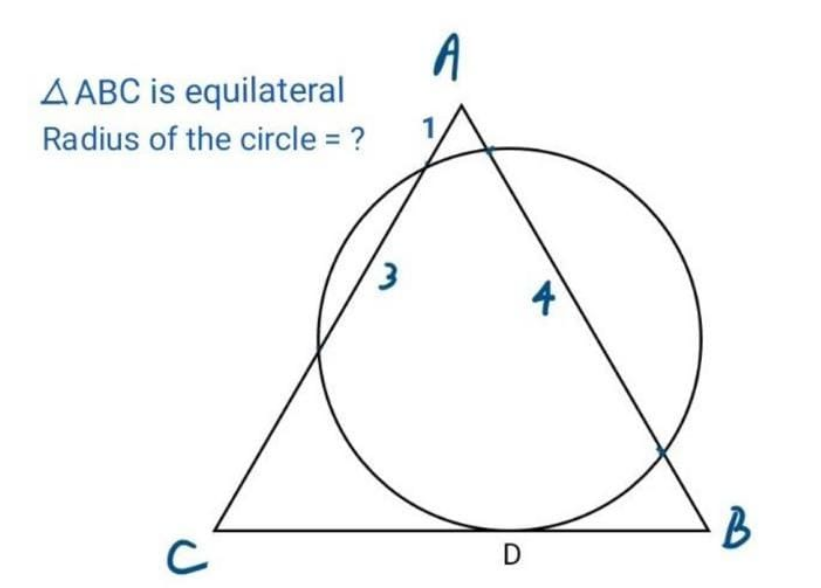


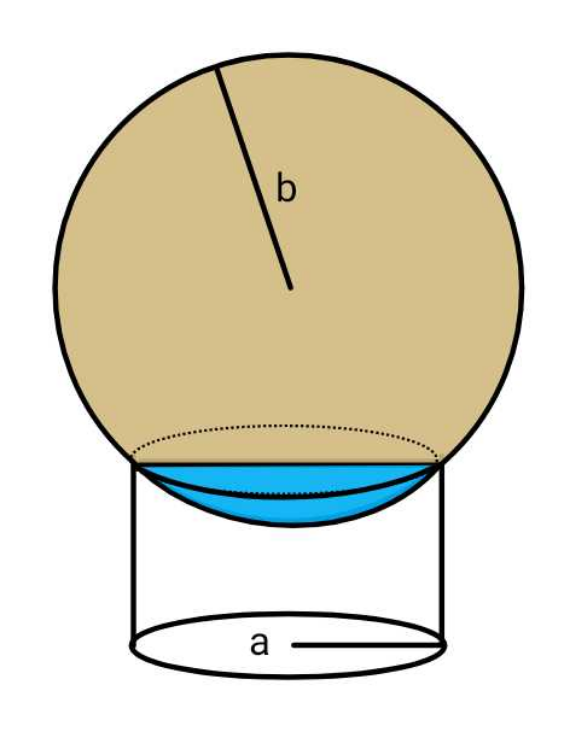

Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237
|
Question and Answers Forum |
AllQuestion and Answers: Page 233 |
| Ques. 2 (Metric Space Question) Let d be a metric on a non−empty set X. Show that the function U is defined by U(x,y)=((d(x,y))/(1+d(x,y))), where x and y are arbitrary element X is also a metric on X. |
| Ques. 1 (Metric Space Question) Let X = ρ_∞ be the set of all bounded sequences of complex numbers. That is every element of ρ_∞ is a complex sequence x^− ={x^− }_(k=1) ^∞ such ∣x_i ∣<Kx^− , i=1,2,3,... where Kx is a real number which may define on x for an arbitrary x^− ={x_i }_(i=1) ^∞ and y^− ={y_i }_(i=1) ^∞ in ρ_∞ we define as d_∞ (x,y)=Sup∣x_i −y_i ∣, Verify that d_∞ is a metric on ρ_(∞.) |

|

|

|

|
| Verify that ┐(p→q)→(p∧^┐ q) is tautology using laws of algebra |
| Show that lim_((x,y)→(0,0)) ((x^2 −y^2 )/(x^2 +y^2 )) does not exist |
| Find the relative maximum and minimum of the function f(x,y)=x^3 +y^3 −3x−12y+20 |
| Use laws of algebra to prove the following (a)[(B−A)u(A−B)]=[(AuB)−(AnB)] (b)A▽(AnB)=A−B |
| ∫_0 ^(2π) 3sintcost dt |

|

|

|

|

|

|
| What is the remainder f 149! when divided by 139? |

|
| Divide a 113mm line into ratio 1:2:4 |
| Find the remainder of 67! when divided by 7! |

|
| Solve for x : (x − (1/x))^(1/2) + (1 − (1/x))^(1/2) = x |
| ∫ ((√x)/( (√((1−x^2 )^3 ))))dx = ? |
| 2^a +4^b +8^c =328 find a,b and c when(a,b,c)is natual number |

|
Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 |