
Question and Answers Forum
AllQuestion and Answers: Page 311
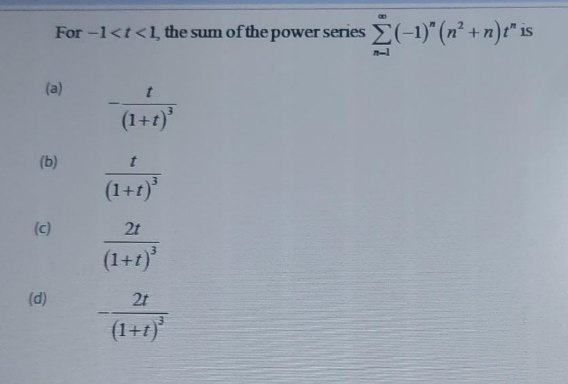

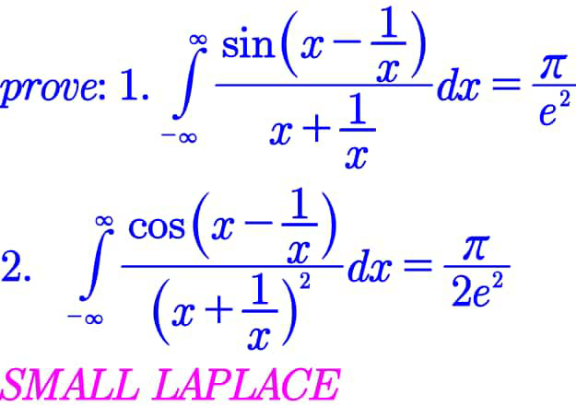


Pg 306 Pg 307 Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315
|
Question and Answers Forum |
AllQuestion and Answers: Page 311 |
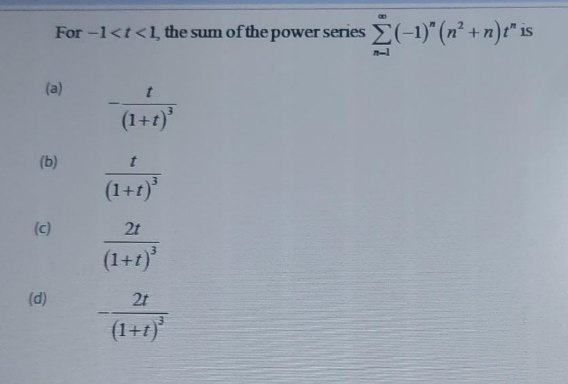
|
| Find the real number satisfying x=(√(1+(√(1+(√(1+x)))))) |
| An odd function f(x) whose domain is R satisfies f(x)=f(x+2). When x ∈ (0, 1), f(x)=−2x^2 +ax−2. If f has 2023 zeros in [0, 1011]. Then the range of a can be ? A. [−6, −2(√2)] B. [−4, −2(√2)] C. [−8, −6] D. [−6, −4] |

|
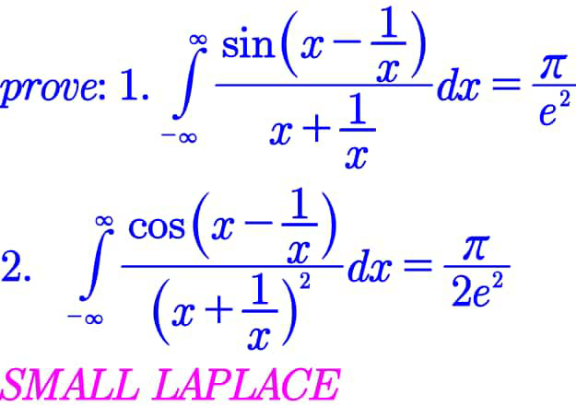
|
| x ∈ [−0,5 ; 0,5] find the product of all x′s 3(cos^2 πx + sinπy) + 2 = 9 + 3 ∣sinπx ∙ sinπy∣−sinπy |
| Lim_( x→∞) x^( 4) ( 1− cos (1− cos((2/x))))=? |
| Σ_(n=o) ^(+oo) (((−1)^n x^(2n+1) )/(4n^2 −1)) |
| f(x)= (√( ∣ x_ ^ ∣ −∣ x−_ ^ ⌊ax⌋ ∣)) ; a ∈ [ 3 , 4 ) find : { (( D_( f) =? (domain ))),(( R_( f) =? (range ))) :} |
| x ∈ [−0,5 ; 0,5] find the product of all x′s 1. 4sin^2 πx−4sinπx + 2 = 2sin^2 πy−1 2. 4sinπx = 4sinπy − 7 − (1/(sin^2 πx)) |

|

|
| xy − 3x = 27 −5y find all (x , y) in Z^2 |
| Given the acceleration a=−4sin2t, initial velocity v(0)=2, and the initial position of the body as s(0)=−3, find the body′s position at time t. Hi |
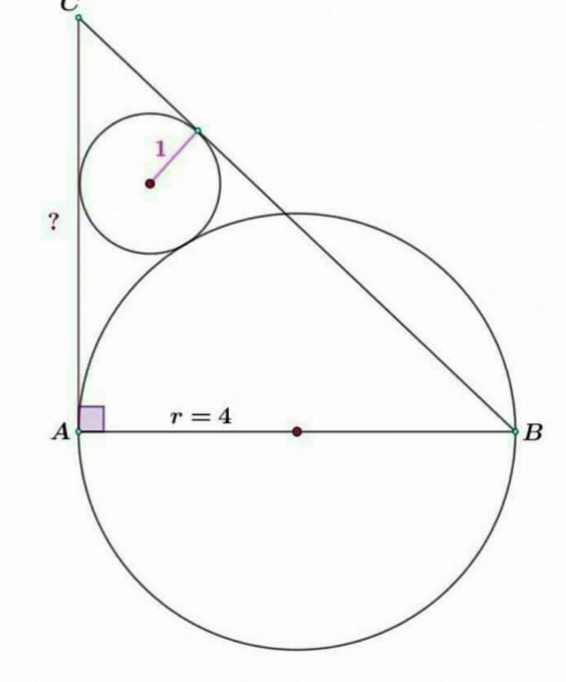
| Find x in terms of c ∀ 0<c<(2/(3(√3))) (3x^2 −1)(3x^2 +36x−1)^2 ={4(x^3 −x−c)+9(7x^2 +1)}^2 |
| Lim_( x→ 0^( +) ) (( 1− cos ( 1− cos((√x) )))/x^( 4) ) |

|
| For 0≤x≤1 , maximum value of f(x)=x(√(1−x+(√(1−x)))) is __ |
| Show that lim_(x→0) (x/(∣x∣)) does not exist |
| Show that lim_(x→0) ((e^(1/x) −1)/(e^(1/x) +1)) does not exist |
| Evaluate lim_(x→(π/6)) (((√3)sin x−cos x)/(x−(π/6))) |
| Evaluate lim_(x→0) ((1−cos x(√(cos 2x)) )/x^2 ) |
| Evaluate lim_(x→2) ((x^5 −32)/(x^3 −8)) |
| Evaluate lim_(x→2) ((x^2 −4)/( (√(3x−2))−(√(x+2)))) |
| Evaluate lim_(x→0) ((tan x−sin x)/(sin^3 x)) |
| Evaluate lim_(x→0) ((e^x +e^(−x) −2)/x^2 ) |
Pg 306 Pg 307 Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 |