
Question and Answers Forum
AllQuestion and Answers: Page 324


Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328
|
Question and Answers Forum |
AllQuestion and Answers: Page 324 |
| Find the equation of the line which is tangent to the parabola y^2 =12x and forms an angle of 45° with the line y=3x−4. |
| find the value of cofficent μ in the following system from the determinat: 2x_1 +μx_2 +x_3 =0 (μ−1)x_1 −x_2 +2x_3 =0 4x_1 +x^2 +4x^3 =0 |
| determine eigenvalues and digonalize by row operation [(4,(−9),6,(12)),(9,(−1),4,6),(2,(−11),8,(16)),((−1),( 3),0,(−1)) ] |
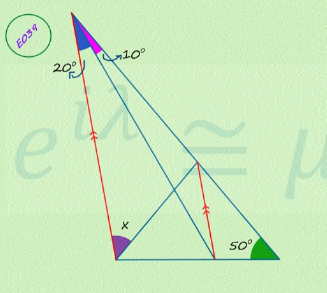
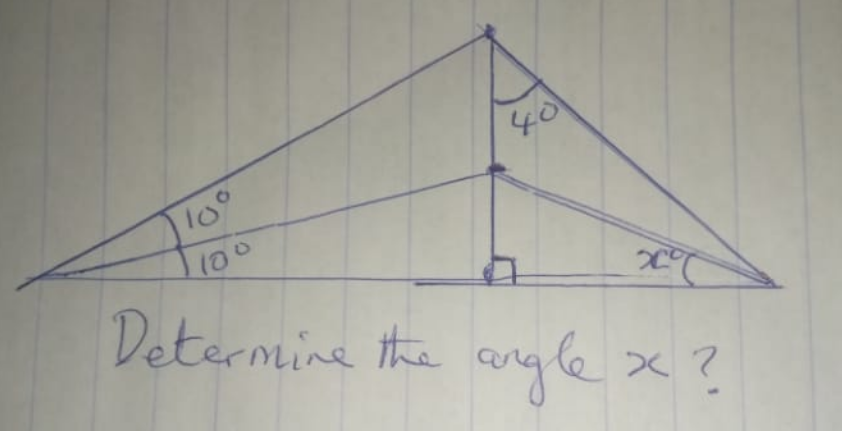
| dererminer la valeur x? |

|

|
| y^((iv)) +16y^((iii)) +9y^((ii)) +256y^((i)) +256y=0 M.m |
| (d^3 y/dx^3 )+4(d^2 y/dx^2 )+(dy/dx)−6y=0 M.m |
| Solve the Differential equation below (d^3 y/dx^3 )+8(d^2 y/dx^2 )+12(dy/dx)=0 M.m |
| Find the coefficient of x^(11) in (2x^2 +x−3)^6 . |
| ax^3 +bx^2 +c=0 x_1 = x_2 = x_3 = |

|

|
| prove that (0/0)=1 |
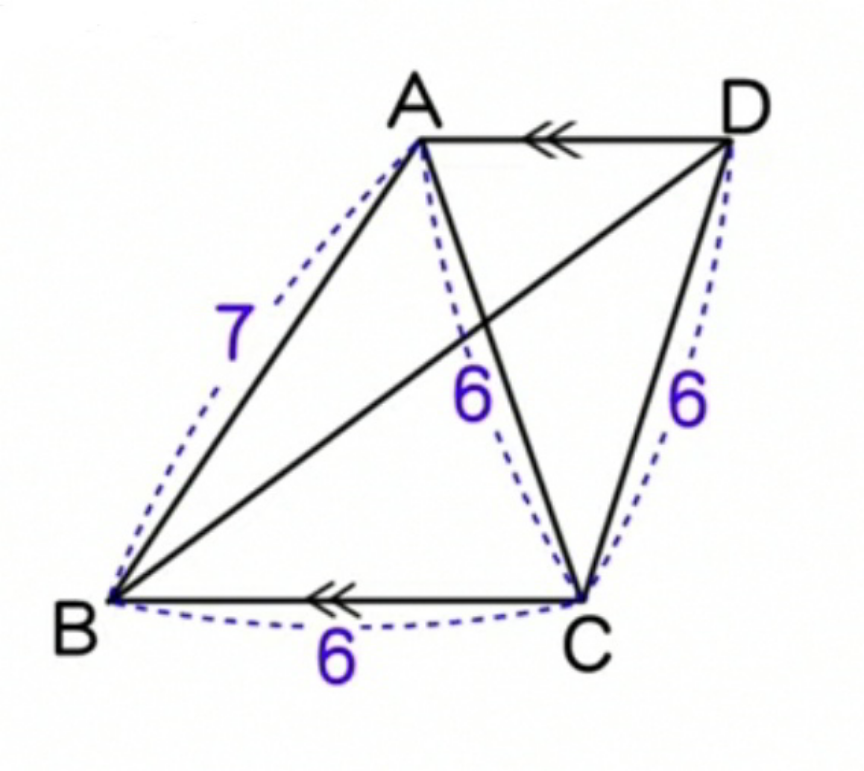
| In the given figure E is the mid point of AB. IF the area of ΔEBF is 8cm^2 .find the area of the parallelogram ABCD. |

|
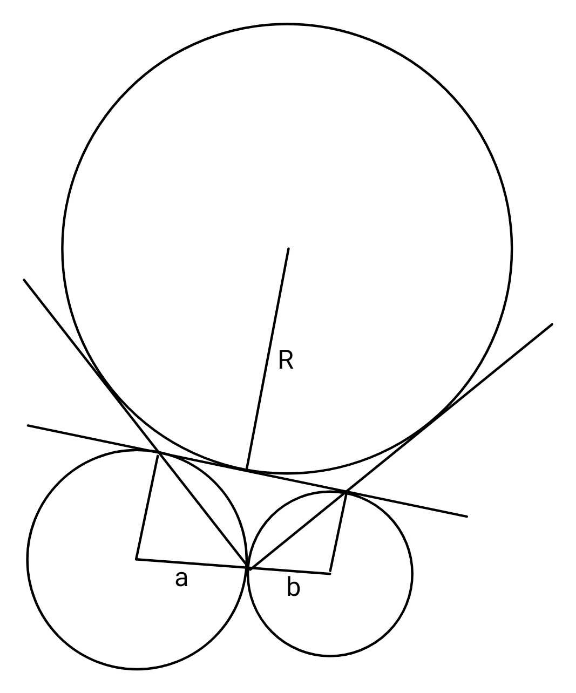
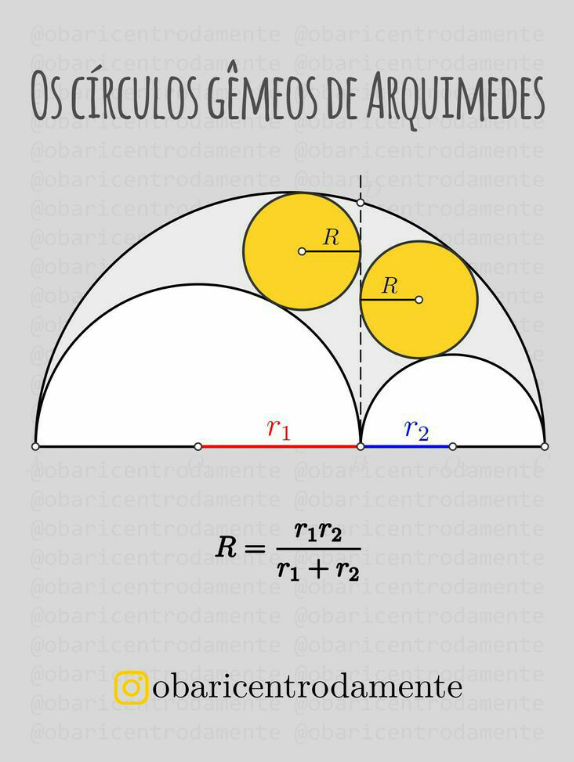
| In △ABC the following relationship holds: (m_b /b) + (m_c /c) ≤ (a/(2r)) ≤ (n_b /h_b ) + (n_c /h_c ) |

|
| Given f(x)= (([(1/3)x]∣2x∣+Ax)/(∣4−x^2 ∣)) if f ′(−1)= 5 then A=? [ ] = floor function |
| ∫ (dx/( ((x^3 +2019))^(1/3) )) =? |
| ∫ ((sin 2x dx)/(sin x−sin^2 2x)) =? |
| lim_(x→0) ((sinx−x)/x^3 )=? |

|
| ∫ln(tanx)dx |

|
| I−Incenter in △ABC A(2,2) , B(6,4) , C(4,8) , M(8,6) Find: MI = ? |
Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328 |