
Question and Answers Forum
AllQuestion and Answers: Page 371









Pg 366 Pg 367 Pg 368 Pg 369 Pg 370 Pg 371 Pg 372 Pg 373 Pg 374 Pg 375
|
Question and Answers Forum |
AllQuestion and Answers: Page 371 |
| Recommended books for trigonometry from zero? I know most Euclidean geometry, and basic algebra. I feel a bit lost |

|

|

|

|

|

|
| Find a, b, c ∈ N ; 2^( a) + 4^( b) + 8^( c) = 328 |
| What is the smallest three digit number divisible by (2/3), (7/9), (4/(13)) without a remainder ? |

|

|

|
| Determiner la hauteur DE(r+x) en fonction de r r=OOC=BH BF=20 pour que distance(AB+BC+CD+DE+EF soit sgale AC+arcCDF |

|
| a_(n+2) −5a_(n+1) +6a_n =3n+5^n a_1 =1, a_2 =0 find a_n |
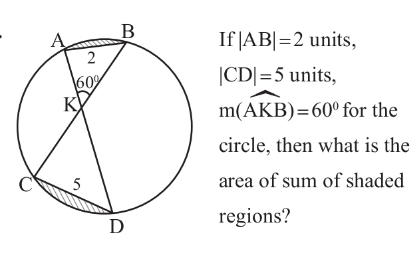
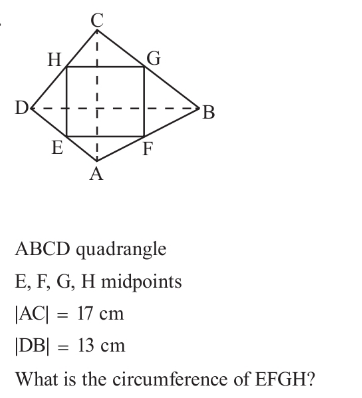
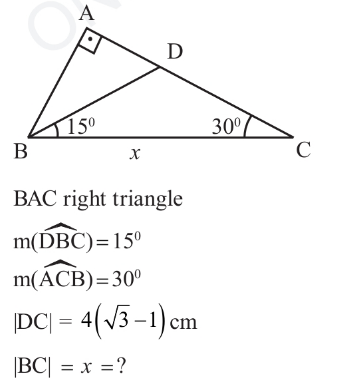
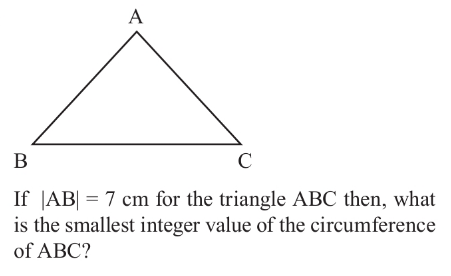
| In the following figure, if ((S_1 +S_2 )/( (√S_3 ))) = (6/( (√π))) find the area of the circular crown |
| In △ABC the following relationship holds: 6r Σ_(cyc) (r_a /(s + n_a )) + Σ_(cyc) n_a ≥ 3s |
| donner la forme trigonometrique(i−1)^5 /(i−4)^4 |
|
| (((√(11))+1)/(2(√(11))+11)) = ((((√(11))+1)(2(√(11))−11))/((2(√(11))+11)(2(√(11))−11))) = ((2(√(11))−11+2×11+11(√(11)))/(2×11−121)) = ((13(√(11))+11)/(−99)) Ans |
| x^3 +y^3 =z^2 x^3 +z^3 =y^2 y^3 +z^3 =x^2 obviously x=y=z=0∨(1/2) trying to totally solve it let y=px∧z=qx (p^3 +1)x^3 =q^2 x^2 (q^3 +1)x^3 =p^2 x^2 (p^3 +q^3 )x^3 =x^2 ⇒ x=0 ⇒ y=0∧z=0 ★ x=(q^2 /(p^3 +1)) x=(p^2 /(q^3 +1)) x=(1/(p^3 +q^3 )) ⇒ (p^2 /(q^3 +1))=(q^2 /(p^3 +1)) (p^2 /(q^3 +1))=(1/(p^3 +q^3 )) ========== p^5 +p^2 −q^5 −q^2 =0 p^5 +p^2 q^3 −q^3 −1=0 subtracting both p^2 (q^3 −1)+q^5 −q^3 +q^2 −1=0 (q−1)(p^2 (q^2 +q+1)+q^4 +q^3 +q+1)=0 ⇒ q=1 ⇒ p^5 +p^2 −2=0 (p−1)(p^4 +p^3 +2p+2)=0 ⇒ p=1 ⇒ x=y=z=(1/2) ★ p^4 +p^3 +2p+2=0 no useable exact solutions p≈−.975564±.528237i ⇒ x≈.33635∓.515329i ∧ y≈−.0559113±.680406i ∧ z=x ★ p≈.475564±1.18273i ⇒ x≈−.586346±.562464i ∧ y≈−.944089∓.426001i ∧ z=x ★ p^2 (q^2 +q+1)+q^4 +q^3 +q+1=0 p^2 =−(((q+1)^2 (q^2 −q+1))/(q^2 +q+1)) we can be sure that (q≠−1⇒p=0) ⇒ p^2 <0 ⇒ p=±(√((q^2 −q+1)/(q^2 +q+1)))(q+1)i ...I′ll continue later |

|

|
| a_(n+2) −3a_(n+1) +2a_n =n+3^n please find a_n |

|
Pg 366 Pg 367 Pg 368 Pg 369 Pg 370 Pg 371 Pg 372 Pg 373 Pg 374 Pg 375 |