
Question and Answers Forum
AllQuestion and Answers: Page 381







Pg 376 Pg 377 Pg 378 Pg 379 Pg 380 Pg 381 Pg 382 Pg 383 Pg 384 Pg 385
|
Question and Answers Forum |
AllQuestion and Answers: Page 381 |
| ∫(([cos^(−1) x{(√((1−x^2 )))}]^(−1) )/(log_e {1+(((sin[2x(√((1−x^2 ))) ])/π) }))dx |
| Solve the differential equation (1+y^2 )dx−(1+x^2 )xydy=0 |
| Solve: (dy/dx)=((y^2 −3xy−5x^2 )/x^2 ) y(1)=−1 M.m |

|
| Q: prove that the following equation has no solution. (√(x +⌊ x ⌋)) + (√(x −(√x) )) = 1 |
| cos(5x)= a.cos^( 5) (x)+b.cos^( 4) (x)+c.cos^3 (x)+ d.cos^( 2) (x)+e.cos(x)+f a , b , c , d , e , f =? |

|

|
| x^(99) +y^(99) = x^(100) Interger solutions? |
| Ω = ∫_0 ^( (π/2)) (( sin( 3x ))/( (√( 1− sin(x).cos(x))))) dx = 2((√( a)) .ln( 1 + (√(b )) ) + c ) find the value of : a + b + c = ? ■ m.n |

|
| the domain of f(x) = (√(log_x {x})) ; {.} denote the fractional part is |

|
| ∫(1/(4t^3 +3t^2 +4t+1))dt |

|
| ∫ (dx/(csc x+ cos x)) =? |

|
| min f(x)=(√(x^2 −2x+5)) +(√(4x^2 −4x+10)) |
| let p(x) = x^6 +ax^5 +bx^4 +cx^3 +dx^2 +ex+f be a polynomial function such that p(1) = 1 ; p(2) = 2 ; p(3) = 3 p(4) = 4 ; p(5) = 5 ; p(6) = 6 then find p(7) = ? |

|
| If 0<a≤b then prove that: determinant ((1,a,(log(a^a ))),(1,((√((a^2 +b^2 )/2)) (√((a^2 +b^2 )/8)) ∙ log(((a^2 +b^2 )/2))),),(1,b,(log(b^b ))))≥ 0 |
|
| in AB^Δ C prove that: sin ((( A)/2) ) ≤ (( a)/( b + c)) ■ |
| ∫_0 ^2 x^t dt=3 solve for x |
| lim_(x→∞) ((x^(1−sin ((1/x))) .(x^(sin ((1/x))) −1))/(ln x)) |
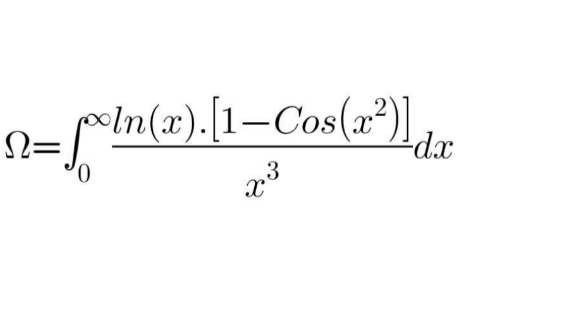
|
Pg 376 Pg 377 Pg 378 Pg 379 Pg 380 Pg 381 Pg 382 Pg 383 Pg 384 Pg 385 |