
Question and Answers Forum
AllQuestion and Answers: Page 389









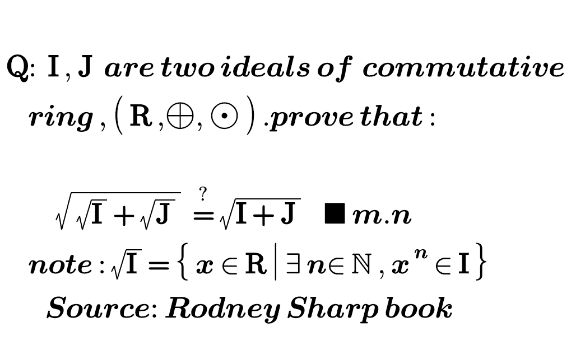
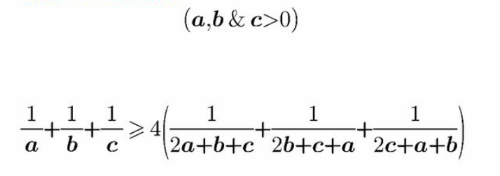
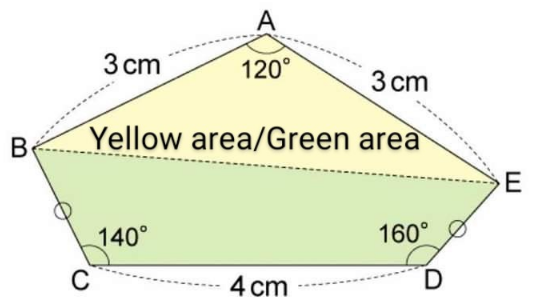

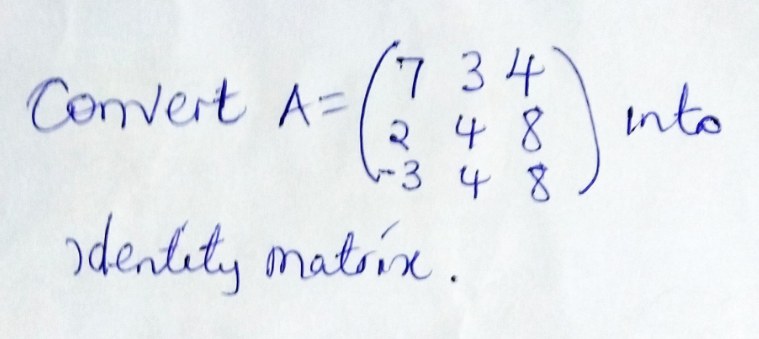

Pg 384 Pg 385 Pg 386 Pg 387 Pg 388 Pg 389 Pg 390 Pg 391 Pg 392 Pg 393
|
Question and Answers Forum |
AllQuestion and Answers: Page 389 |

|
| We know that vertex form of parabola is given as y = a(x−h)^2 +k From the given diagram of bridge that resembles a parabola, we have a vertex points of (0, 30) and other points due to towers that supports the parabolic−shape cable, which is (200, 150). ∴ y = a(x−0)^2 +30 = ax^2 +30 To find the value of ′a′, let′s use the given points other than vertex 150 = a(200)^2 + 30 150−30 = 40000a a = ((120)/(40,000)) = (3/(1000)) ∴ y = ((3x^2 )/(1000)) +30 Also, since we′re asked to find a function that gives a length of metal rod needed relative to its distance from the midpoint of the bridge, with each rods have an equal distance to each other, then we must consider another variable ′d′ that represents the equal distance of metal rods relative to its decided quantity and variable ′n′ given as positive integer that divides the distance of midpoint to tower. d = ((200)/n) ⇒ nd = 200 Example: Engineers decided to use 8 metal rodus, then we have d = ((200)/8) = 25 To calculate the length of each rods, let′s use the formula above First rod: y = ((3(0∙25)^2 )/(1000)) +30 = 30 ft. Second rod: y = ((3(1∙25)^2 )/(1000)) +30 = 31.875 ft. Third rod: y = ((3(2∙25)^2 )/(1000)) +30 = 37.5 ft. Fourth rod: y = ((3(3∙25)^2 )/(1000)) +30 = 46.875 ft. |
| Given f(x)=x^4 +ax^3 +bx^2 +cx+d where a,b,c and d are real number suppose the graph f(x) intersects the graph of y=2x−1 at x=1,2,3. Find the value of f(0)+f(4). |
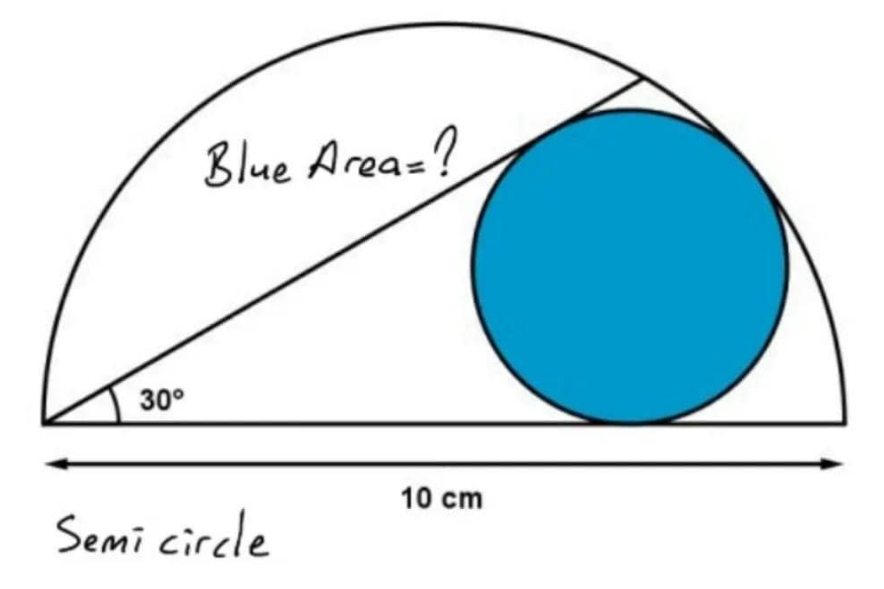
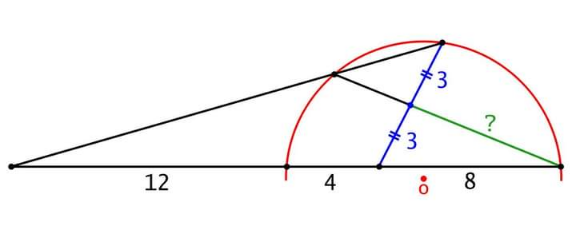
| Please solve . |
| For which value of x this cubic equation will be 0 ? a^3 − 16a − 3 |

|

|

|

|

|

|
| ∫(((sinx)/( (√x))))dx Mastermind |

|

|
| Q: by using fourier series, prove that : 𝛀=Σ_(n=1) ^∞ (((−1)^( n−1) )/((2n−1 )^( 3) )) = (𝛑^( 3) /(32)) −−−−−− |

|

|
| where am i wrong ? |
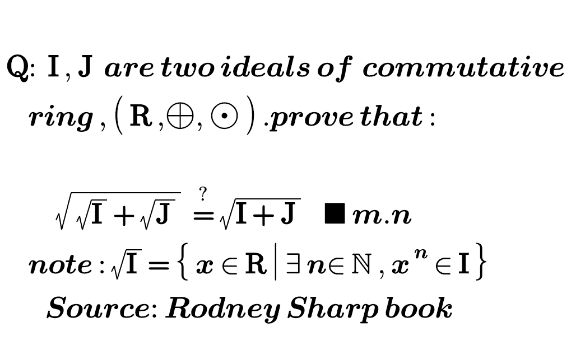
|
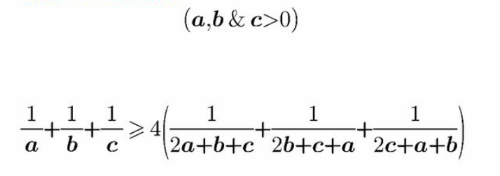
|

|
| ≪_• ^• I THINK...^ ^(−) _•^• _(−) ≫ One question per post, IDEAL 👍👍👍 Two questions per post,OK (BEARABLE) (👎+👍)/2 Three or more questions:NO, NO, NO! 👎👎👎 |
| A graduating student keeps applying for a job until she gets an offer. The probability of getting an offer at any trial is 0.35. What is the expected number of applications? |

|
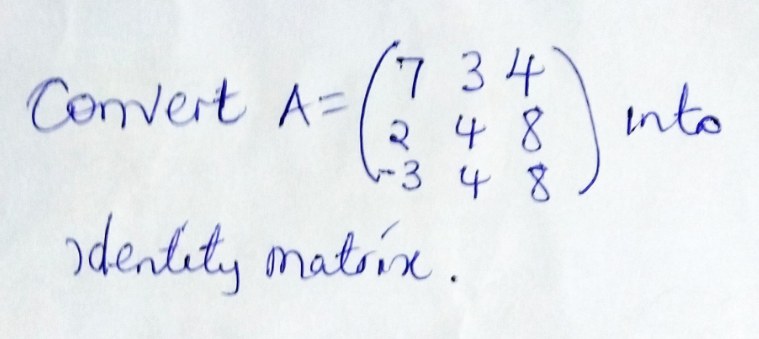
|

|
Pg 384 Pg 385 Pg 386 Pg 387 Pg 388 Pg 389 Pg 390 Pg 391 Pg 392 Pg 393 |