Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 452

Question Number 168812 Answers: 0 Comments: 0

∫_0 ^π (sin x)^(cos x) dx

$\int_{0}^{π} {(\sin x)}^{\cos x} d x$

Question Number 168801 Answers: 0 Comments: 6

Question Number 168800 Answers: 0 Comments: 1

If the function f is continuous in [a,b] express lim_(n→∞) (1/n)Σ_(k=1) ^n f((k/n)) as a definite integral.

$If the function f is continuous in [a, b]$ $express \lim_{n \to \infty} \frac{1}{n} \underset{k = 1}{\sum^{n}} f (\frac{k}{n}) as a definite$ $integral .$

Question Number 168799 Answers: 0 Comments: 0

If the function f is continuous in [a,b] prove that lim_(x→∞ ) ((b−a)/n)Σ_(k=1) ^n f(a+((k(b−a))/n))=∫_a ^b f(x)dx

$If the function f is continuous in$ $[a, b]$ $prove that$ $\lim_{x \to \infty} \frac{b - a}{n} \underset{k = 1}{\sum^{n}} f (a + \frac{k (b - a)}{n}) = \int_{a}^{b} f (x) d x$

Question Number 168788 Answers: 0 Comments: 1

Question Number 168787 Answers: 0 Comments: 1

Question Number 168781 Answers: 0 Comments: 1

Question Number 168776 Answers: 1 Comments: 4

Question Number 168823 Answers: 2 Comments: 0

Q#168480 reposted. n^2 +n+109=x^2 x∈Z, n(∈Z^+ )=?

$You can't use 'macro parameter character #' in math mode$ $n^{2} + n + 109 = x^{2}$ $x \in Z, n (\in Z^{+}) = ?$

Question Number 168772 Answers: 1 Comments: 1

Question Number 168771 Answers: 0 Comments: 0

Question Number 168762 Answers: 0 Comments: 2

Question Number 168755 Answers: 0 Comments: 5

∫(1/(x+(√(1−x)))) dx

$\int \frac{1}{x + \sqrt{1 - x}} d x$

Question Number 168753 Answers: 0 Comments: 1

∫(dx/( (√(sin^(−1) (x)))))=?

$\int \frac{d x}{\sqrt{{s i n}^{- 1} (x)}} = ?$

Question Number 168745 Answers: 1 Comments: 1

∫(1/(x+(√(x−1)))) dx = ??

$\int \frac{1}{x + \sqrt{x - 1}} d x = ? ?$

Question Number 168744 Answers: 3 Comments: 0

Resolve 1) ∫((√(1+cos x))/(sin x))dx 2) ∫(dx/(1+((x+1))^(1/3) )) 3) ∫((xtan x)/(cos^4 x))dx 4) ∫(dx/(1+(√x)+(√(1+x))))

$R e s o l v e$ $1) \int \frac{\sqrt{1 + \cos x}}{\sin x} d x$ $2) \int \frac{d x}{1 + \sqrt[3]{x + 1}}$ $3) \int \frac{x \tan x}{\cos^{4} x} d x$ $4) \int \frac{d x}{1 + \sqrt{x} + \sqrt{1 + x}}$

Question Number 168743 Answers: 1 Comments: 1

∫_0 ^∞ ((√t)/(1+t^2 ))dt FAILED TO CALCULATE

$\int_{0}^{\infty} \frac{\sqrt{t}}{1 + t^{2}} d t$ $FAILED TO CALCULATE$

Question Number 168742 Answers: 1 Comments: 0

Resolve y=xy′+a(√(1+(y′)^2 ))

$R e s o l v e$ $y = {x y}^{'} + a \sqrt{1 + {(y^{'})}^{2}}$

Question Number 168737 Answers: 1 Comments: 1

Question Number 168734 Answers: 0 Comments: 0

Question Number 168732 Answers: 2 Comments: 0

Question Number 168723 Answers: 0 Comments: 2

Resolve (x+5)^5 y^(′′) =1

$R e s o l v e$ ${(x + 5)}^{5} y^{^{″}} = 1$

Question Number 168722 Answers: 0 Comments: 1

Resolve x^2 y^(′′) +xy^′ +y=1

$R e s o l v e$ $x^{2} y^{^{″}} + {x y}^{^{'}} + y = 1$

Question Number 168721 Answers: 1 Comments: 0

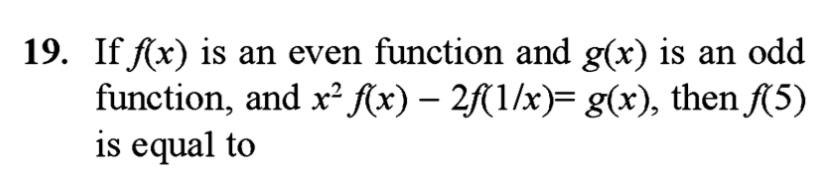
Question Number 168710 Answers: 0 Comments: 4

Question Number 168709 Answers: 0 Comments: 3

Pg 447 Pg 448 Pg 449 Pg 450 Pg 451 Pg 452 Pg 453 Pg 454 Pg 455 Pg 456

Contact: info@tinkutara.com