
Question and Answers Forum
AllQuestion and Answers: Page 487
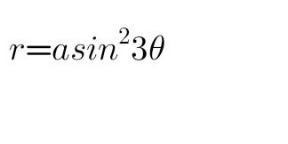

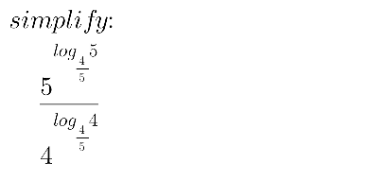
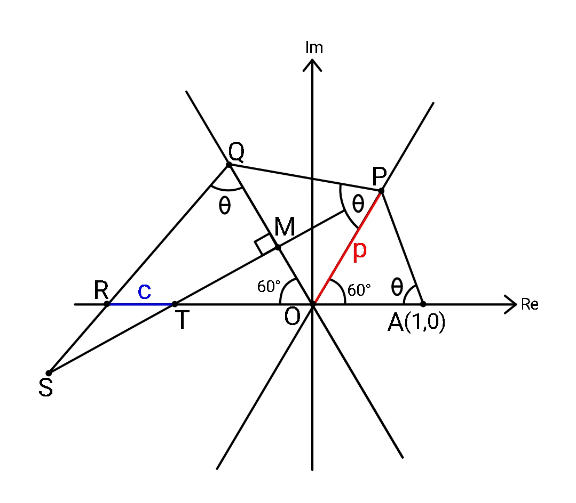
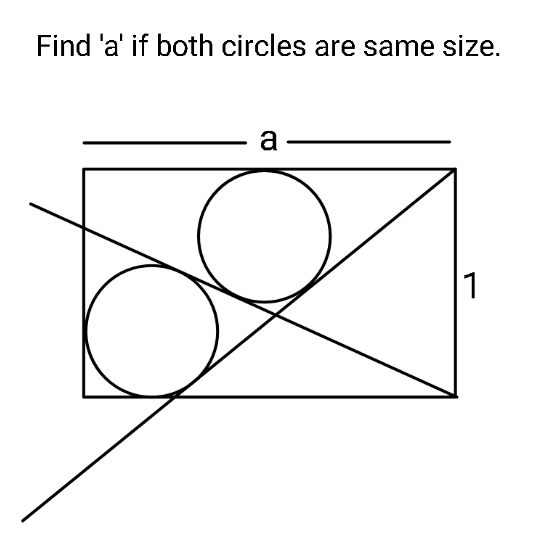





Pg 482 Pg 483 Pg 484 Pg 485 Pg 486 Pg 487 Pg 488 Pg 489 Pg 490 Pg 491
|
Question and Answers Forum |
AllQuestion and Answers: Page 487 |
| soit la serie de fonction Σ_(n=2 ) (x^n /(nx+ln(n))) etudie la convergence simple sur [0,1[ |
|

|
|

|
| Σ_(i=1) ^(n=∞) lim_(x→0) ((xyn^x )/(nx_1 ))xz∫((xn^n x)/(nx^n y))dn (√(c^n +n_1 )) ∫((xn^(n!) )/(n^n xn^x ))dn |
| make x the subject of the formula; a^x +bx+c=0 |

|
| Question by M.N July Φ = ∫_0 ^( 1) ((ln(1 + x^4 + x^8 ))/x)dx Φ =^(x=x^(1/2) ) (1/2)∫_0 ^( 1) ((ln(1+x^2 +x^4 ))/x)dx Φ = (1/2)∫_0 ^( 1) ((ln(((1−x^2 )/(1−x^6 ))))/x)dx = (1/2)∫_0 ^( 1) ((ln(1−x^2 ))/x)dx − (1/2)∫_0 ^( 1) ((ln(1−x^6 ))/x)dx Φ = (1/2)(A − B) A =^(x=x^(1/2) ) (1/2)∫_0 ^( 1) ((ln(1−x))/x)dx = (1/2)Li_2 (1) B =^(x=x^(1/6) ) (1/6)∫_0 ^( 1) ((x^((1/6)−1) ln(1−x))/x^(1/6) )dx B = (1/6)∫_0 ^( 1) ((ln(1−x))/x)dx = (1/6)Li_2 (1) Φ = (1/2)((1/2)Li_2 (1)−(1/6)Li_2 (1)) = (1/6)Li_2 (1) 𝚽 = ((𝛇(2))/3) ▲▲▲ |
| Find: Σ_(n=1) ^∞ tan^(−1) ((1/n^2 )) |
| Σ_(n=4) ^∞ 2 × ((3/4))^(n+3) |
| Find: Σ_(n=1) ^k ((n^2 sin^2 ((nπ)/2))/(n^4 π^4 + n^2 π^2 a + b)) = ? |
| lim_(x→1_(y→2) ) x^2 +y^2 =? |
| ∫_0 ^( 2π) ln ( 1+ cos (x)).cos (nx )dx=? |
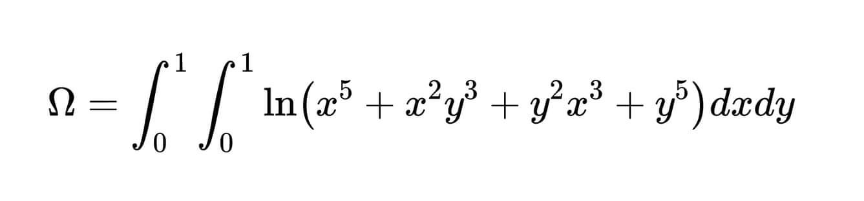
|
| x∈R ⇒ ∣ log _2 ((x/2))∣^3 +∣log _2 (2x)∣^3 =28 |

|

|

|
| f(x)=2x^2 +5x. Montrer que f est lipschitzienne sur R. |
| f(x)=2x^2 +5x. Montrez que f est uniformement continue sur R. |
| f(x+f(x))=3f(x) and f(−1)=7 faind f(27)=? |

|

|

|
| Let , f : [ 0 , 1 ] → R is a continuous function , prove that : lim_( n→ ∞) ∫_0 ^( 1) (( n f(x))/(1+ n^2 x^( 2) )) dx = (π/2) f (0 ) −−− proof −−− S_( n) = [∫_(0 ) ^( (1/( (√n)))) (( n. f(x))/(1 + n^( 2) x^( 2) )) dx =Ω_( n) ]+[ ∫_(1/( (√n))) ^( 1) ((n.f (x))/(1 + n^( 2) x^( 2) )) dx = Φ_( n) ] Ω_( n) =_(∃ t_( n) ∈ ( 0 , (1/( (√n) )) )) ^(MeanValueTheorem( first)) f (t_( n) )∫_(0 ) ^( (1/( (√n)))) (( n)/(1 + n^( 2) x^( 2) ))dx = f ( t_( n) ) ( tan^( −1) ( (√n) )) lim_( n→∞) (Ω_( n) ) = (π/2) f (lim_( n→∞) ( t_( n) ) ) = (π/2) f (0 ) Φ_( n) = ∫_(1/( (√n))) ^( 1) (( n. f(x) )/(1 + n^( 2) x^( 2) )) dx ⇒_(∃ M >0) ^(f is bounded) ∣ Φ_( n) ∣ ≤ M.∫_(1/( (√n))) ^( 1) (n/(1+ n^( 2) x^( 2) )) dx ⇒ ∣ Φ_( n) ∣ ≤ M . ( tan^( −1) ( n )− tan^( −1) ( (√n) )) lim_( n→ ∞) ∣ Φ_( n) ∣ = 0 ⇒ lim_( n→∞) Φ_( n) =0 ∴ lim_( n→ ∞) ( S_( n) ) = (π/2) f (0 ) ■ m.n |
Pg 482 Pg 483 Pg 484 Pg 485 Pg 486 Pg 487 Pg 488 Pg 489 Pg 490 Pg 491 |