
Question and Answers Forum
AllQuestion and Answers: Page 513







Pg 508 Pg 509 Pg 510 Pg 511 Pg 512 Pg 513 Pg 514 Pg 515 Pg 516 Pg 517
|
Question and Answers Forum |
AllQuestion and Answers: Page 513 |

|
| [reposted] find ∫_( 0) ^( (𝛑/2)) sin^8 (x)dx + ∫_( 0) ^( 1) sin^(-1) ((x)^(1/8) ) dx=? |
| put the digits 0,1,2,3,4,5,6,7,8,9,in place of the letters in order to perform the edditon |
| calculate Ω = Σ_(n=1) ^∞ (( (−1)^( n) n)/(3^( n) (2n −1 ))) =? − Inspired from Sir Ghaderi′s post− |

|
| Prove that: ∫_( 0) ^( (𝛑/4)) ((4 ln (cotx))/(cos(2x + 2022𝛑))) dx = 3𝛇(2) |
| Prove ∫_( 0) ^( (𝛑/2)) sin^8 (x) + ∫_( 0) ^( 1) sin^(-1) ((x)^(1/8) ) ≥ (π/2) |
| Prove the Identity for any (a,n) in Real Number (1 + a)∙a^([n]) = a ∙ a^(2[(n/2)]) + a^(2[((n+1)/2)]) [∗] Greatest Integer Function |
| Prove the identity for any ′n′ in Real number [(n/2)] ∙ [((n + 1)/2)] = (1/4)([n]^2 + 2[(n/2)] - [n]) [∗] Greatest Integer Function |
| ∫(dx/((a−cosx)^2 )) a>1 |
| lim_(x→0) ((7tan x−tan 7x)/(3x)) =? |
| find Σ_(n=1) ^∞ (((−1)^n )/(n^3 (2n+1)^4 )) |
| Let m & n be two positive numbers greater than 1 . If lim_(p→0) ((e^(cos (p^n )) −e)/p^m ) = (1/2)e then (n/m)=? |
| lim_(x→0) ((∫_0 ^1 (arctan (t+sin x)−arctan t)dt)/(arctan x))=? |

|

|

|

|
| prove that ψ′′ ((1/4) )= −2π^( 3) − 56 ζ (3 ) |
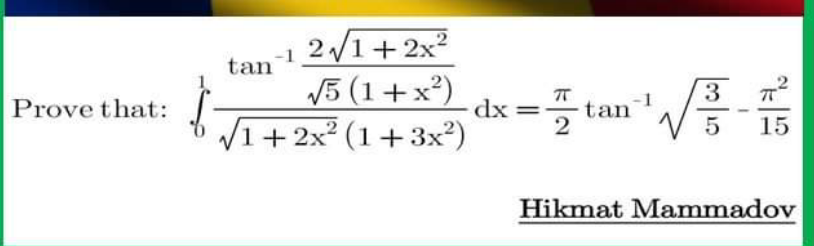
|
| If x ∈R the maximum value of ((3x^2 +9x+17)/(3x^2 +9x+7)) is ... |

|
| Let x_1 ,x_2 ,x_3 be the roots of the equation x^3 +3x+5=0 . Then the value of expression (x_1 +(1/x_1 ))(x_2 +(1/x_2 ))(x_3 +(1/x_3 )) is equal to |
| Given that the solution set of the quadratic inequality ax^2 +bx+c >0 is (2,3). Then the solution set of the inequality cx^2 +bx+a <0 will be |
| ∫_0 ^1 ∫_0 ^1 ∫_0 ^1 ln^2 (x+y+z)dxdydz=? |
| lim_(x→0) ((5sin x−sin 3x cos 2x−cos 3x sin 2x)/x^3 ) =? |
Pg 508 Pg 509 Pg 510 Pg 511 Pg 512 Pg 513 Pg 514 Pg 515 Pg 516 Pg 517 |