
Question and Answers Forum
AllQuestion and Answers: Page 530

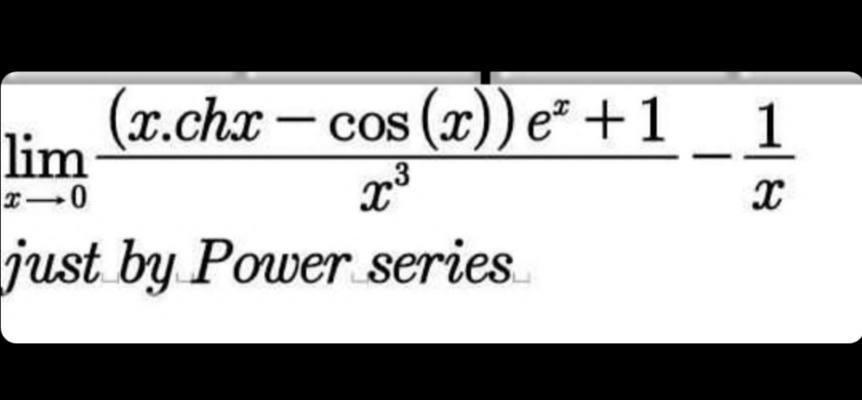


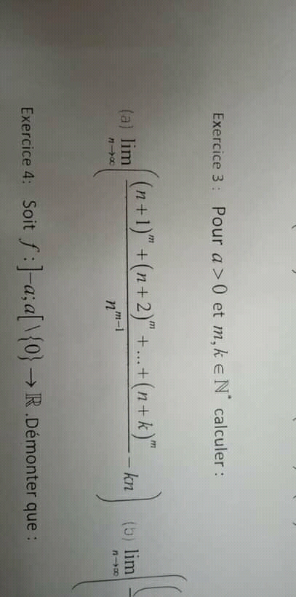
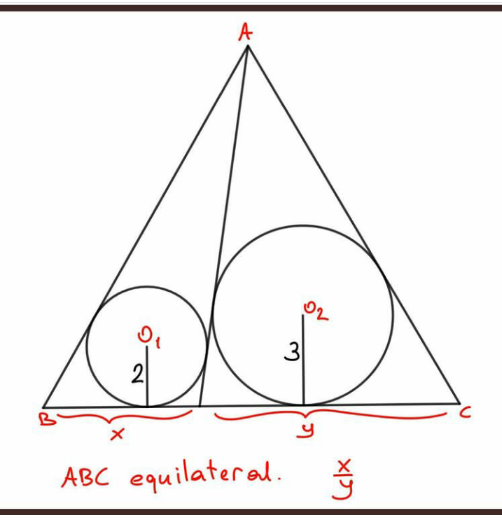






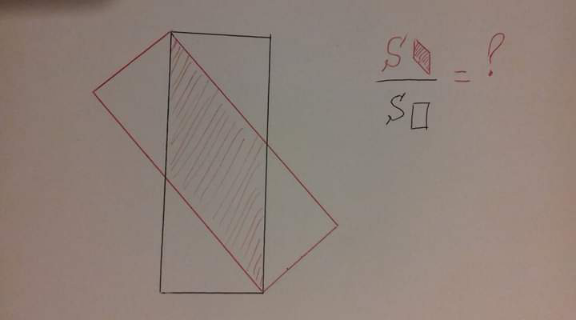
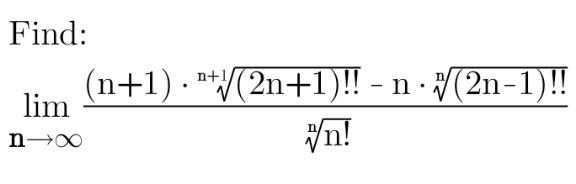
Pg 525 Pg 526 Pg 527 Pg 528 Pg 529 Pg 530 Pg 531 Pg 532 Pg 533 Pg 534
|
Question and Answers Forum |
AllQuestion and Answers: Page 530 |

|
| (x^2 +x−12)^3 +(x^2 +3x−18)^2 = 9(x^2 −9)^2 x=? |
| nature de cette integrale quequ′en soit le reel α ∫_1 ^(+oo) t^α e^(−t) dt |
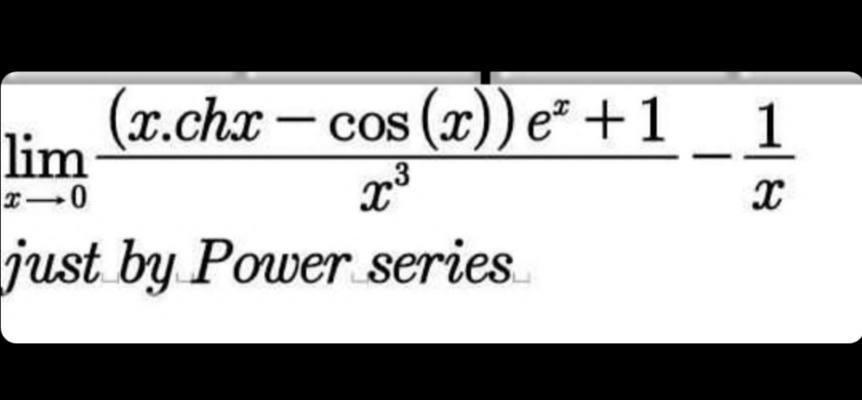
|
| # Advanced Calculus # Φ = ∫_0 ^( 1) (((ln^ ( (1/(1− x)) ))/x) )^( 3) dx =^? 3 ( ζ (2 ) + ζ (3 )) −−−− solution−−−− Φ =^(I.B.P) [ (( 1)/(2x^( 2) )) ln^( 3) ( 1−x)]_0 ^1 +(3/2) ∫_0 ^( 1) (( ln^( 2) (1− x ))/(x^( 2) (1 − x ))) dx = (1/2) lim_( ξ →1^(− ) ) ((ln^( 3) ( 1− ξ ))/ξ^( 2) ) +(3/2)[∫_0 ^( 1) (( ln^( 2) ( 1− x ))/x)dx = 2 ζ (3)] + (3/2)[∫_0 ^( 1) (( ln^( 2) ( 1−x))/x^( 2) ) dx = (π^( 2) /3) = 2ζ (2 )] +(3/2)∫_0 ^( 1) (( ln^( 2) (1− x))/(1−x)) dx} =(1/2) lim_( ξ →1^( −) ) {((ln^( 3) ( 1−ξ ))/ξ^( 2) ) −ln^( 3) (1− ξ ) } +(3/2) (2ζ (3 )) +(3/2) ( 2ζ (2 )) = 3( ζ (3 ) + 3ζ (2 ) ) ■ m.n |

|

|
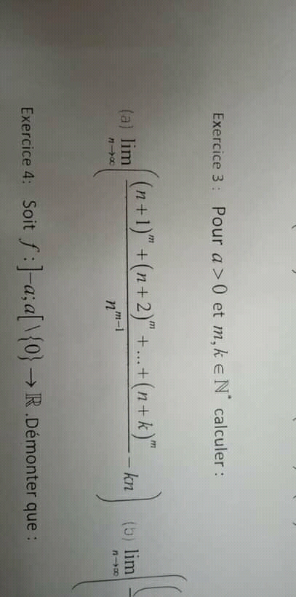
|
| solve (d^2 y/dx^2 )−y=x^2 sin3x |

|
| −1≤a_0 ≤b_0 ≤c_0 ≤1 ∀n∈N a_(n+1) =∫_(−1) ^1 min(x,b_n ,c_n )dx b_(n+1) =∫_(−1) ^1 mil(x,a_n ,c_n )dx c_(n+1) =∫_(−1) ^1 max(x,b_n ,a_n )dx mil(a,b,c) est le terme median de (a,b,c) nature de (a_n ),(b_n ),(c_n ) |

|
| Solve for real numbers: (((x^2 +3n^2 )/(4n^2 )))^4 = (2/n) y-1 ; (((x^2 +3n^2 )/(4n^2 )))^4 = (2/n) z-1 (((x^2 +3n^2 )/(4n^2 )))^4 = (2/n) x-1 n ∈ (0 ; ∞) fixed |
| Be p a prime number , arbitrary. Solve on positive integers (x;y;z) { ((xy + z^2 = 3p + 4)),((x + yz^2 = p + 4)) :} |

|

|

|

|
| Prove that 1 + (1/( (√2))) + (1/( (√3))) + …+ (1/( (√n))) < 2(√n) |

|

|
| { ((((x+y)/(xyz)) = −(1/4))),((((y+z)/(xyz)) = −(1/(24)))),((((x+z)/(xyz)) = (1/(24)))) :} |
| Calculate lim_(x→0) ((tgx^m )/((sin x)^n )), lim_(x→0) ((xcos x−x)/((e^x −1)ln (1+3x^2 ))) |
| please ∫((lnx)/(x+lnx))dx calculate. |
| In how many ways can you divide 20 students into 5 groups with 4 students in each group such that any two students don′t meet each other in more than one group. |
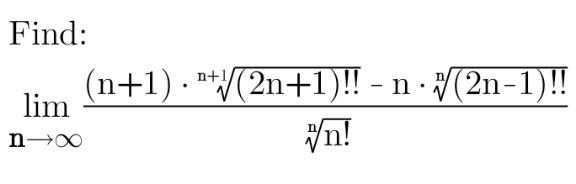
|
Pg 525 Pg 526 Pg 527 Pg 528 Pg 529 Pg 530 Pg 531 Pg 532 Pg 533 Pg 534 |